题目内容
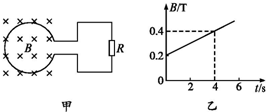
如图甲所示,一个n=10匝,面积为S=0.3m2的圆形金属线圈,其总电阻为R1=2Ω, 与R2=4Ω的电阻连接成闭合电路。线圈内存在方向垂直于纸面向里,磁感应强度按B1=2t + 3 (T)规律变化的磁场。电阻R2两端通过金属导线分别与电容器C的两极相连.电容器C紧靠着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒。圆筒内壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径为r=0.4m.
(1)金属线圈的感应电动势E和电容器C两板间的电压U;
(2)在电容器C内紧靠极板且正对a孔的D处有一个带正电的粒子从静止开始经电容器C加速后从a孔垂直磁场B2并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒.已知粒子的比荷q/m=5×107(C/kg),该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子重力和空气阻力,则磁感应强度B2 多大(结果允许含有三角函数式)。
(1) 6V ;4V (2) 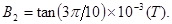 或
或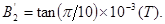
【解析】
试题分析:(1)线圈中产生的感应电动势E= 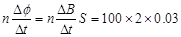 V
=6V
V
=6V
电容器C两板间电压U=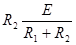 =4V
=4V
(2)据动能定理有, 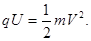
带电粒子在磁场中作匀速圆周运动,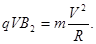
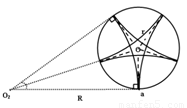
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为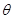 ,则由几何关系可得:
,则由几何关系可得:
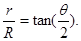
有两种情形符合题意(如图所示):
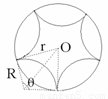
(ⅰ)情形1:每段轨迹圆弧对应的圆心角为 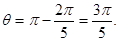
得: 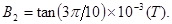
(ⅱ)情形2:每段轨迹圆弧对应的圆心角为 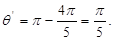
将数据代式得: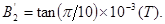
考点:此题考查法拉第电磁感应定律、欧姆定律及动能定理;考查的物理模型是匀速圆周运动。

 阅读快车系列答案
阅读快车系列答案


 如图甲所示,一个圆形线圈的匝数n=100,线圈面积S=200cm2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图已所示.下列说法中正确的是( )
如图甲所示,一个圆形线圈的匝数n=100,线圈面积S=200cm2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图已所示.下列说法中正确的是( )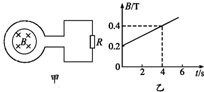 如图甲所示,一个圆形线圈的匝数n=1 000,线圈面积S=300cm2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,线圈处在有一方向垂直线圈平面向里的圆形磁场中,圆形磁场的面积S0=200cm2,磁感应强度随时间的变化规律如图乙所示.求:
如图甲所示,一个圆形线圈的匝数n=1 000,线圈面积S=300cm2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,线圈处在有一方向垂直线圈平面向里的圆形磁场中,圆形磁场的面积S0=200cm2,磁感应强度随时间的变化规律如图乙所示.求: