��Ŀ����
����Ŀ����ֱ������ϵxOy�У���һ�����ڴ�����y�Ḻ������н�糡�����е������߽�ֱ���Ox��Oy�غϣ��糡ǿ�ȴ�СΪE���ڵڶ��������д�ֱֽ��������н�ų���ͼ��δ���������ų��߽�Ϊ���Σ����е�һ���߽���y���غϣ��Ÿ�Ӧǿ�ȵĴ�СΪB��һ����Ϊm������Ϊq�������ӣ��ӵ糡��P����ij���ٶ���-x����ʼ�˶����������꣨0��L����Q��ʱ���ٶȴ�СΪ![]() ��������-y�����30�㣬���ų�ƫת���ܹ����ص糡�������������ơ���
��������-y�����30�㣬���ų�ƫת���ܹ����ص糡�������������ơ���
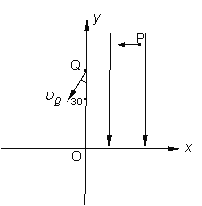
��1����������P��ij��ٶȣ�
��2�����δų�����С�����
��3�������ڷ��ص糡ǰ�˶����ʱ�䡣
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
��������
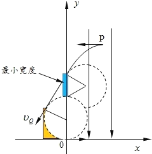
(1)�����ڴ�P��Q�ڵ糡������������ƽ���˶���
���ڣ�vQ=![]()
���ԣ�v0=vX=vQsin30=![]()
(2)�����뿪�ų�����ֱ�ӽ���ų�ƫת�ص糡��Ҳ������ֱ���˶�һ�ξ�����ٽ���ų�ƫת�ص糡��
���ڣ�![]()
���ԣ�R=L/3
�����뿪�糡��ֱ�ӽ���ų�ƫתԲ�Ľ�60
��С���ȣ���x=![]()
��С�߶�Ϊ��y=2Rsin30=L/3
���ΪS=��x��y=![]()
(3)�����뿪�糡����ֱ���˶����ٽ���ų������ͨ��O�㷵�ص糡�ڵ糡�����Ŵų��������ƣ������ڴų�ƫת��Բ�Ľ������˶�ʱ��䳤��
�ڴų���ƫת�ʱ��t:
t=T/3=![]()