题目内容
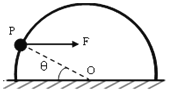
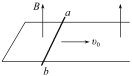
【题目】如图所示，两根平行的光滑金属导轨与水平面成53°放置，两导轨上端接了一个
Ω的定值电阻，导轨电阻忽略不计，在水平虚线P、Q间有一与导轨所在平面垂直的匀强磁场B，磁场区域的宽度为d = 1.0 m．导体棒
、b的质量分别为
、
，电阻
。现将它们分别从图中M、N处同时由静止释放，两棒向下滑动中与导轨始终垂直且接触良好，当
刚穿出磁场时，正好进入磁场，且都是匀速穿过磁场区域。取重力加速度g = 10m/s2，sin53° = 0.8，cos53° = 0.6，不计电流间的相互作用，求：
（1）从开始释放起到棒刚穿出磁场止，这个过程中，导体棒上消耗的电能？
（2）从开始释放起到
两棒相遇所用的时间以及相遇点与Q的距离（结果可以用分数表示）
【答案】（1）1.04J（2）
；
m
【解析】
根据金属杆的受力平衡即安培力等于重力的分力解出两杆的安培力大小，克服安培力做功等于重力所做的功；根据运动学关系式解出两杆的间距。
（1）a、b匀速经过磁场时受安培力
b棒克服安培力做功，系统产生的电能分别为：
a、b匀速经过磁场时,电路结构相同：电源内阻
b匀速过磁场时b棒消耗电能
a匀速过磁场时b棒消耗电能
即b棒共消耗电能Q=1.04J
（2）由
则联立前面可得
由
得
a进磁场前加速时间
a匀速经过磁场用时
在a匀速过磁场时b加速位移
得
此时b速度变为
则相遇时有
得
即从开始到相遇共用时
此时相遇点离Q间距x=
gsin53
练习册系列答案
黄冈冠军课课练系列答案
相关题目
