Question

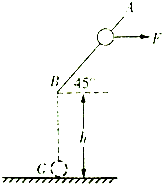如图所示，竖直面内固定一根与水平方向成45°角的光滑直杆AB，杆B端正下方h处有一点C．有一质量为m的小球套在直杆上，始终受到一个水平向右的恒力作用（恒力未知），现让小球以某一速度沿杆匀速下滑，小球离开杆在空中运动一段时间后恰好到达C点（忽略空气阻力）．已知重力加速度为g，求：
（1）小球离开直杆后运动的加速度大小；
（2）小球沿杆下滑时的速度大小．

Answer 1

分析：（1）根据牛顿第二定律可求得加速度的大小；
（2）小球离开B点后，水平方向上做的是先减速以后加速，在竖直方向上是加速运动．

解答：解：（1）小球匀速下滑，受力平衡，可得：F=mg  
当小球脱离直杆后合力为：F=

2

mg
由牛顿第二定律可得：a=

F

m

=

2

g
（2）小球从B点运动到C点的过程中，水平方向有：t=

2vx

g

竖直方向有：h=v_yt+

1

2

gt²
由速度分解可得：v_x=v_y=

2

2

v
解得：v=

2

2

gh

．
答：（1）小球离开直杆后运动的加速度大小为

2

g；
（2）小球沿杆下滑时的速度大小为

2

2

gh

．

点评：本题第一问比较简单，根据物体的受力情况可以求得加速度的大小，小球离开B后在竖直方向上受重力的作用，做加速运动，在水平方向上受恒力F的作用，做的也是匀变速运动．