题目内容
我国“嫦娥二号”探月卫星于2010年10月1日成功发射，有一阶段在离月球表面h高度处的圆形轨道上运行．已知“嫦娥二号”在该轨道上运行的周期为T，月球半径为R，月球表面处的重力加速度为g，引力常量为G．根据以上信息，不可求出（ ）
分析：探月卫星做匀速圆周运动，万有引力定律提供向心力，用周期表示的向心力与用线速度表示的向心力相等，则可求出线速度的大小，利用球体体积公式和密度公式可求出平均密度，利用重力等于万有引力可求出引力加速度的大小．
解答：解：A、探月卫星做匀速圆周运动，根据周期与线速度的关系，即：v=
，所以A选项可以求出．故A错误；
B、因为不知卫星的质量，因此无法知道卫星的动能大小，故B正确．
C：探月卫星受到的万有引力提供向心力，
=
=ma．a=
．故C错误．
D：探月卫星受到的万有引力提供向心力，
=
，又因月球的体积V=
πR3，月球的质量与体积、平均密度关系：ρ=
，
联立求得平均密度为：ρ=
，故D错误．
故选：B
| 2π(R+h) |
| T |
B、因为不知卫星的质量，因此无法知道卫星的动能大小，故B正确．
C：探月卫星受到的万有引力提供向心力，
| GMm |
| (R+h)2 |
| 4π2m(R+h) |
| T2 |
| 4π2(R+h) |
| T2 |
D：探月卫星受到的万有引力提供向心力，
| GMm |
| (R+h)2 |
| 4π2m(R+h) |
| T2 |
| 4 |
| 3 |
| M |
| V |
联立求得平均密度为：ρ=
| 3π(R+h)3 |
| GT2R3 |
故选：B
点评：解答本题知道探月卫星所受的万有引力提供向心力，利用周期与线速度表示向心力，然后结合万有引力定律、球体体积公式、密度公式求解，还要知道重力近似等于万有引力求引力加速度．解答时注意公式间的化简．
练习册系列答案
相关题目
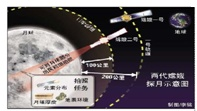“嫦娥二号”是我国月球探测第二期工程的先导星，目前已经完成各项技术攻关，将于今年10月份发射．“嫦娥二号”原本是“嫦娥一号”的备份卫星，因此两颗星在外形和重量上并没有太大差别．不过它的绕月飞行轨道将由“嫦娥一号”时的200公里高度降低到100公里，这样就能把月球看得更清楚．她们绕月球运动的示意图如右图所示（轨道视为圆周），则下列有关探月卫星的说法正确的是（ ）| A、“嫦娥二号”卫星绕月球运行的动能小于“嫦娥一号”卫星绕月球的动能 | B、“嫦娥二号”卫星在图示轨道上运行时的加速度大于月球表面的重力加速度 | C、“嫦娥二号”卫星所在位置的重力加速度比“嫦娥一号”所在位置的重力加速度大 | D、“嫦娥一号”卫星在绕月轨道上经过加速变轨可达到“嫦娥二号”的绕月轨道 |
=
