题目内容
一质量为m的人站在电梯中，电梯加速上升，加速度大小为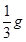
（g为重力加速度）。人对电梯底部的压力大小为
A． | B．2mg | C．mg | D． |
D
解析试题分析：分析人受力，受重力与支持力，由牛顿第二定律：N－G＝ma，则N＝G+ma=，根据牛顿第三定律，则人对电梯底部的压力为。
考点：本题考查牛顿运动定律。
津桥教育计算小状元系列答案一斜块M静止于粗糙的水平面上，在其斜面上放一滑块m，若给m一向下的初速度v0，则m正好保持匀速下滑，如图(6)所示，现在m下滑的过程中再加一个作用力，则以下说法正确的是（ ）
| A．在m上加一竖直向下的力Fa，则m将保持匀速运动，M对地仍无摩擦力的作用 |
| B．在m上加一沿斜面向下的力Fb，则m将做加速运动，M对地有水平向左的静摩擦力 |
| C．在m上加一水平向右的力Fc，则m将做减速运动，在m停止前M对地仍无摩擦力的作用 |
| D．无论在m上加上什么方向的力，在m停止前M对地都无静摩擦力的作用 |
如图，某人正通过定滑轮将质量为m的货物提升到高处．滑轮的质量和摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图所示．由图可以判断正确的是（ ）
A．图线与纵轴的交点M的值 ． |
| B．图线与横轴的交点N的值． |
| C．图线的斜率等于物体的质量m． |
| D．图线的斜率等于物体质量的倒数1／m． |
关于速度、加速度、合力间的关系，正确的是( )
| A．物体的速度越大，则物体的加速度越大，所受合力也越大 |
| B．物体的速度为零，则物体的加速度一定为零，所受合力也为零 |
| C．物体的速度为零，加速度可能很大，所受的合力也可能很大 |
| D．物体的速度很大，加速度一定很大，所受的合力可能为零 |
如图所示，在半径为R的四分之一光滑圆弧轨道的顶端a点，质量为m的物块（可视为质点）由静止开始下滑，经圆弧最低点b滑上粗糙水平面，圆弧轨道在b点与水平轨道平滑相接,物块最终滑至c点停止。若物块与水平面问的动摩擦因数为μ,下列说法正确的是（ ） 
A．物块滑到b点时的速度为 |
| B．物块滑到b点时对b点的压力是2mg |
C．c点与b点的距离为 |
| D．整个过程中物块机械能损失了mgR |
如图所示，把小车放在倾角为30°的光滑斜面上，用轻绳跨过定滑轮使之与盛有沙子的小桶相连，不计滑轮质量及摩擦，已知小车的质量为3m，小桶与沙子的总质量为m，小车从静止释放后，在小桶上升竖直高度为h的过程中（ ）
| A．小桶处于失重状态 |
B．小桶的最大速度为 |
| C．小车受绳的拉力等于mg |
| D．小车的最大动能为mgh |
在匀强电场中，有一质量为m，带电量为q的带电小球静止在O点，然后从O点自由释放，其运动轨迹为一直线，直线与竖直方向的夹角为θ，如图所示，那么关于匀强电场的场强大小的下列说法中正确的是：
A．唯一值是 | B．最大值是 |
C．最小值是 | D．不可能是 |
物理学中有些问题的结论不一定必须通过计算才能验证，有时只需要通过一定的分析就可以判断结论是否正确。如图所示，倾角为θ的足够长的粗糙斜面固定在水平地面上，质量为M的木块上固定一轻直角支架，在支架末端用轻绳悬挂一质量为m的小球。由静止释放木块，木块沿斜面下滑，稳定后轻绳与竖直方向夹角为α，则木块与斜面间的动摩擦因数为 （ ） 
| A．μ=tanθ | B．μ= tanα |
| C．μ= tan(θ-α) | D．μ= tan(θ+α) |