题目内容
10. 如图,质量为m的小物体静放在质量为M的小车的平板左端,车与地面间摩擦不计,一次给物体一个向右的速度v,另一次给 小车一个向左的速度v,若小车质量M大于物体质量m,则两次最后物体和小车间达到相对静止时( )
如图,质量为m的小物体静放在质量为M的小车的平板左端,车与地面间摩擦不计,一次给物体一个向右的速度v,另一次给 小车一个向左的速度v,若小车质量M大于物体质量m,则两次最后物体和小车间达到相对静止时( )| A. | 速度的大小相等 | B. | 所需时间相等 | ||
| C. | 小车走过的距离相等 | D. | 物体相对小车滑行的距离相等 |
分析 两次运动过程中,小车和物体所受外力之和为零,系统动量守恒,根据动量守恒定律求解相对静止时的共同速度,根据牛顿第二定律求解小车和物体的加速度,再根据匀变速直线运动基本公式求解时间和小车运动的位移,根据能量守恒定律求解物体相对小车滑行的距离.
解答 解:A、第一次给物体一个向右的速度v,物体与车相对静止时的速度为v1,此过程中系统动量守恒,以向右为正方向,根据动量守恒定律得:
mv=(M+m)v1
解得:${v}_{1}=\frac{mv}{M+m}$,
同理,给小车一个向左的速度v,物体与车相对静止时的速度为v2,此过程中系统动量守恒,以向左为正方向,根据动量守恒定律得:
Mv=(M+m)v2
解得:${v}_{2}=\frac{Mv}{M+m}$,所以速度大小不等,故A错误;
B、设小车与物体间的摩擦力为f,第一次,根据牛顿第二定律得:${a}_{1}=-\frac{f}{m}$,运动的时间${t}_{1}=\frac{{v}_{1}-v}{{a}_{1}}=\frac{\frac{mv}{M+m}-v}{-\frac{f}{m}}$=$\frac{Mmv}{(m+M)f}$,
第二次,对小车,根据牛顿第二定律得:${a}_{2}=-\frac{f}{M}$,运动时间${t}_{2}=\frac{{v}_{1}-v}{{a}_{2}}=\frac{\frac{Mv}{M+m}-v}{-\frac{f}{M}}=\frac{Mmv}{(m+M)f}$,则运动时间相等,故B正确;
C、小车第一次做匀加速直线运动和第二次做匀减速直线运动的加速度相等,但是初末位置速度不等,根据$2ax={v}^{2}-{{v}_{0}}^{2}$可知,运动的位移不等,故C错误;
D、根据能量守恒定律得:
$\frac{1}{2}m{v}^{2}-\frac{1}{2}(M+m){v}_{1}^{2}=f•△{x}_{1}$,
$\frac{1}{2}M{v}^{2}-\frac{1}{2}(M+m){{v}_{2}}^{2}=-f△{x}_{2}$,
联立解得:△x1=△x2,故D正确.
故选:BD
点评 本题主要考查了动量守恒定律以及能量守恒定律得直接应用,解题时注意要规定正方向,明确运动过程中损失的能量等于摩擦力乘以相对位移,难度适中.

| A. | 甲灯亮些 | B. | 乙灯亮些 | C. | 两灯一样亮 | D. | 无法判定 |
 如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )| A. | 着地时两物体速度相同 | B. | 着地时两物体机械能相同 | ||
| C. | 着地时两物体所受重力的功率相同 | D. | 两物体沿斜面滑行的时间相同 |
| A. | 电源电动势等于电源两极间的电压 | |
| B. | 电源电动势与外电路的组成无关,只与电源本身有关 | |
| C. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| D. | 电动势在数值上等于非静电力把1C的正电荷在电源内从负极已送到正极所做的功 |
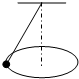 绳长一定,绳的上端固定,下端系一小球,小球在水平面 上做匀速圆周运动,如图,则小球的运动周期T、速率v、角速度ω跟绳与竖直线之间的夹角θ的关系是:θ越大,( )
绳长一定,绳的上端固定,下端系一小球,小球在水平面 上做匀速圆周运动,如图,则小球的运动周期T、速率v、角速度ω跟绳与竖直线之间的夹角θ的关系是:θ越大,( )| A. | T越小 | B. | ω越小 | C. | v越小 | D. | T越大 |
| A. | 加速度反映速度变化的快慢,与速度无关 | |
| B. | 物体加速度越大,速度一定越大 | |
| C. | 加速度就是“增加出来的速度” | |
| D. | 物体速度越大,加速度一定越大 |
 如图所示,是某白炽灯泡的电流I和电压U关系的图象,该灯泡的额定电压为48V,请你根据图象回答下列问题:
如图所示,是某白炽灯泡的电流I和电压U关系的图象,该灯泡的额定电压为48V,请你根据图象回答下列问题: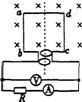 如图所示为一正弦交流发电机的简化图,线圈abcd的面积是0.05m2,共100匝,线圈电阻为1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=$\frac{1}{π}T$,当线圈以300r/min的转速匀速旋转时.求:
如图所示为一正弦交流发电机的简化图,线圈abcd的面积是0.05m2,共100匝,线圈电阻为1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=$\frac{1}{π}T$,当线圈以300r/min的转速匀速旋转时.求: