题目内容
15.A、B两人沿向下运行的自动扶梯跑下楼,相对电梯的速度A为u,B为n u,下楼过程中A跑过p级,B跑过q级,则自动扶梯的级数为(n−1)pq(np−q),速度为nu(q−p)np−q.分析 人的速度分别为u和nu,设自动扶梯的速度为v,自动扶梯总级数为N,A下楼时间为t1,则人的速度乘以下楼时的时间加上自动扶梯的速度乘以下楼时的时间就等于自动扶梯总级数N;
设B下楼时间为t2,则人的速度乘以下楼时的时间加电梯的速度乘以下楼时的时间就等于自动扶梯总级数N;根据以上分析,列出方程解答.
解答 解:A与B的速度分别为:u,nu,设v为电梯的速度,自动扶梯总级数为N,每一级台阶长度为l;
则A下楼的过程中:ut1+vt1=Nl,ut1=pl
B下楼的过程中:nut2+vt2=Nl,nut2=ql
联立以上四个公式得:
N=(n−1)pq(np−q),
v=nu(q−p)np−q
故答案为:(n−1)pq(np−q),nu(q−p)np−q.
点评 解答此题的关键是要明确人的速度要快于自动扶梯的速度,否则他就下不来,此题的难点在于解方程,因此要求学生具备一定的学科综合能力.

练习册系列答案
相关题目
16.两质点运动的速度-时间图象如图所示,下列说法正确的是( )
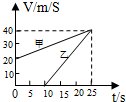

| A. | 在0-10秒内只有甲物体在运动 | |
| B. | 在10秒末乙物体离出发点最近 | |
| C. | 在25秒末两物体相遇 | |
| D. | 不能确定这段时间内两物体的前后位置 |
3.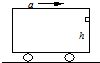 如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )
如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )
 如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )
如图,以速度v匀速行驶的车厢,突然以加速度a作匀加速运动,小球恰从车厢内高度为h的架子上落下,则落在车厢地板上的点距架子的水平距离为( )| A. | 0 | B. | ahg | C. | v√2hg | D. | v√2va |
10. 如图,质量为m的小物体静放在质量为M的小车的平板左端,车与地面间摩擦不计,一次给物体一个向右的速度v,另一次给 小车一个向左的速度v,若小车质量M大于物体质量m,则两次最后物体和小车间达到相对静止时( )
如图,质量为m的小物体静放在质量为M的小车的平板左端,车与地面间摩擦不计,一次给物体一个向右的速度v,另一次给 小车一个向左的速度v,若小车质量M大于物体质量m,则两次最后物体和小车间达到相对静止时( )
 如图,质量为m的小物体静放在质量为M的小车的平板左端,车与地面间摩擦不计,一次给物体一个向右的速度v,另一次给 小车一个向左的速度v,若小车质量M大于物体质量m,则两次最后物体和小车间达到相对静止时( )
如图,质量为m的小物体静放在质量为M的小车的平板左端,车与地面间摩擦不计,一次给物体一个向右的速度v,另一次给 小车一个向左的速度v,若小车质量M大于物体质量m,则两次最后物体和小车间达到相对静止时( )| A. | 速度的大小相等 | B. | 所需时间相等 | ||
| C. | 小车走过的距离相等 | D. | 物体相对小车滑行的距离相等 |

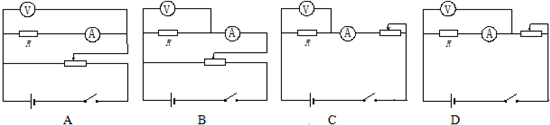
 用伏安法测电池电动势E以及内阻r.按照实验值作出U-I图线,由此图线求得该电池电动势E=2.96V,电源内阻r=0.738Ω.(取3位有效数字)
用伏安法测电池电动势E以及内阻r.按照实验值作出U-I图线,由此图线求得该电池电动势E=2.96V,电源内阻r=0.738Ω.(取3位有效数字)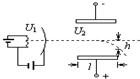 如图是一个说明示波管工作的原理图,电子经加速电场(加速电压为U1)加速后垂直进入偏转电场,离开偏转电场时偏转量是h,两平行板间的距离为d,电压为U2,板长为l,每单位电压引起的偏移
如图是一个说明示波管工作的原理图,电子经加速电场(加速电压为U1)加速后垂直进入偏转电场,离开偏转电场时偏转量是h,两平行板间的距离为d,电压为U2,板长为l,每单位电压引起的偏移