题目内容
【题目】如图所示,质量都为m的A物块和B物块通过轻质细线连接,细线跨过轻质定滑轮,B物块的正下方有一个只能在竖直方向上伸缩且下端固定在水平面上的轻质弹簧,其劲度系数为k,开始时A锁定在固定的倾角为30°的光滑斜面底端,弹簧处于原长状态,整个系统处于静止状态,B物块距离原长状态弹簧上端的高度为H,现在对A解除锁定,A、B物块开始运动,A物块上滑的最大位移未超过固定光滑斜面顶端.已知当A物块上滑过程细线不收缩的条件是 ![]() (重力加速度为g,忽略滑轮与轮轴间的摩擦,弹簧一直处在弹性限度内)下列说法正确的是( )
(重力加速度为g,忽略滑轮与轮轴间的摩擦,弹簧一直处在弹性限度内)下列说法正确的是( )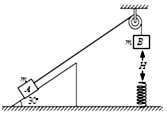
A.当B物块距离弹簧上端的高度 ![]() 时,弹簧最大弹性势能为
时,弹簧最大弹性势能为 ![]()
B.当B物块距离弹簧上端的高度 ![]() 时,A物块上升的最大位移为
时,A物块上升的最大位移为 ![]()
C.当B物块距离弹簧上端的高度 ![]() 时,弹簧最大弹性势能为
时,弹簧最大弹性势能为 ![]()
D.当B物块距离弹簧上端的高度 ![]() 时,A物块上升的最大位移为
时,A物块上升的最大位移为 ![]()
【答案】B,D
【解析】解:AB、当 ![]() 时,绳子恰好不收缩,即B到达最低点时绳子的拉力为零,且两者的加速度大小相等,故对A有:
时,绳子恰好不收缩,即B到达最低点时绳子的拉力为零,且两者的加速度大小相等,故对A有:
mgsin30°=ma,
对B有:F弹﹣mg=ma,
解得: ![]() ,
,
弹簧压缩量: ![]() ,
,
所以B下降的高度即A上升的最大位移为: ![]() ,
,
由于到达最低点两者的速度都为零,减小的重力势能转化为弹簧的弹性势能,故根据功能关系可知弹簧的最大弹性势能为 ![]() ,A不符合题意B符合题意;
,A不符合题意B符合题意;
CD、当 ![]() 时,绳子会收缩,即当B到达最低点时,A会继续沿斜面上升一段距离,当弹簧仍被压缩
时,绳子会收缩,即当B到达最低点时,A会继续沿斜面上升一段距离,当弹簧仍被压缩 ![]() 时,受力和AB选项中的相同,故根据能量守恒定律可得:
时,受力和AB选项中的相同,故根据能量守恒定律可得:
![]() ,
,
A之后的运动由于拉力为零,所以机械能守恒,故有:
![]() ,
,
解得: ![]() ,
,
故A上升的最大位移为: ![]() ,
,
在弹簧弹性势能为 ![]() 时,B仍有
时,B仍有 ![]() 的动能,如果这些动能全部转化为弹性势能,则在最低点弹簧的弹性势能为
的动能,如果这些动能全部转化为弹性势能,则在最低点弹簧的弹性势能为 ![]() ,但B下降过程中重力还做正功,所以弹簧的最大弹性势能大于
,但B下降过程中重力还做正功,所以弹簧的最大弹性势能大于 ![]() ,C不符合题意,D符合题意.
,C不符合题意,D符合题意.
所以答案是:BD
【考点精析】通过灵活运用弹性势能和机械能守恒及其条件,掌握弹性势能是物体由于发生弹性形变而具有的能量;在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变即可以解答此题.

 计算高手系列答案
计算高手系列答案