题目内容
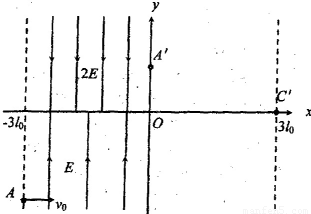
 如图所示在xOy平面中,在直线x=-3l0到y轴区域内存在着两个方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向,x轴上方的场强大小是下方的2倍,y轴右方有垂直于xOy平面的匀强磁场,在电场左边界上点A(-3l0,-2l0)处有一质量为m,电量为q带正电的微粒,以速度v0沿x轴正方向射入电场,其轨迹从y轴上的A′(0,l0)射出电场并进入磁场,并通过x轴上的点C′(3l0,0).不计微粒的重力.
如图所示在xOy平面中,在直线x=-3l0到y轴区域内存在着两个方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向,x轴上方的场强大小是下方的2倍,y轴右方有垂直于xOy平面的匀强磁场,在电场左边界上点A(-3l0,-2l0)处有一质量为m,电量为q带正电的微粒,以速度v0沿x轴正方向射入电场,其轨迹从y轴上的A′(0,l0)射出电场并进入磁场,并通过x轴上的点C′(3l0,0).不计微粒的重力.(1)求微粒在电场中的运动时间t;
(2)求y轴右方的磁感应强度B的大小和方向;
(3)求x轴下方电场强度E.
分析:(1)粒子在左侧的电场中做的是类平抛运动,水平方向上是匀速运动,由匀速运动的规律可以求得粒子的运动的时间;
(2)根据粒子在左侧的电场中做类平抛运动,由动能定理可以求得粒子的速度的大小,粒子在y轴右侧在磁场中做的是匀速圆周运动,根据匀速圆周运动的规律可以求得磁感应强度的大小;
(3)粒子在左侧的电场中做的是类平抛运动,对y轴正负方向分别根据类平抛运动的规律可以求得电场强度的大小.
(2)根据粒子在左侧的电场中做类平抛运动,由动能定理可以求得粒子的速度的大小,粒子在y轴右侧在磁场中做的是匀速圆周运动,根据匀速圆周运动的规律可以求得磁感应强度的大小;
(3)粒子在左侧的电场中做的是类平抛运动,对y轴正负方向分别根据类平抛运动的规律可以求得电场强度的大小.
解答:解:(1)微粒在电场中水平匀速直线运动:3l0=v0t
解得t=
(2)从A到A′电场力做功:Eq2l0-2Eql0=
m(v2-
)
解得 v=v0,
根据粒子水平以v0匀速运动,粒子经过A′时速度是水平的v0,
轨迹r2=(r-l0)2+3
解得r=5l0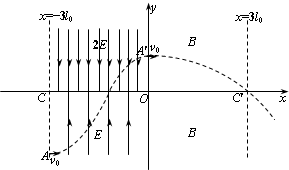
由洛伦兹力提供向心力,qv0B=m
解得B=
,
(3)在x轴下方粒子做类平抛运动,
y负方向,2l0=
×
y正方向,l0=
×
t0=t1+t2=3
,
x方向 3l0=v0t
解得 E=
.
解得t=
| 3l0 |
| v0 |
(2)从A到A′电场力做功:Eq2l0-2Eql0=
| 1 |
| 2 |
| v | 2 0 |
解得 v=v0,
根据粒子水平以v0匀速运动,粒子经过A′时速度是水平的v0,
轨迹r2=(r-l0)2+3
| l | 2 0 |
解得r=5l0

由洛伦兹力提供向心力,qv0B=m
| v2 |
| r |
解得B=
| mvo |
| 5ql0 |
(3)在x轴下方粒子做类平抛运动,
y负方向,2l0=
| 1 |
| 2 |
| qE |
| m |
| t | 2 1 |
y正方向,l0=
| 1 |
| 2 |
| 2qE |
| m |
| t | 2 2 |
t0=t1+t2=3
|
x方向 3l0=v0t
解得 E=
m
| ||
| ql0 |
点评:本题考查带电粒子在匀强磁场中的运动,要掌握住半径公式、周期公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目