题目内容
【题目】如图所示，在倾角为θ=30的光滑斜面上，物块A、B质量均为m。物块A静止在轻弹簧上端，物块B用细线与斜面顶端相连，A、B靠在一起，但A、B之间无弹力。已知重力加速度为g，某时刻将细线剪断，下列说法正确的是
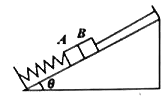
A. 细线剪断前，弹簧的弹力为mg B. 细线剪断前，细线的拉力为mg
C. 细线剪断瞬间，弹簧的弹力发生变化 D. 细线剪断瞬间，物块B的加速度大小为
g
【答案】D
【解析】
本题考查了牛顿第二定律的瞬时问题，抓住剪断细线的瞬间弹簧的弹力不变，剪断细绳前，隔离对A分析，根据共点力平衡求出弹簧的弹力大小，剪断细线的瞬间，弹簧的弹力不变，对整体分析，求出整体的加速度，隔离分析求出A.B间的弹力大小。
A、剪断细绳前，由于A.B之间无弹力，对A分析可以得到弹簧的弹力：
，故A错；
B、剪断细绳前，由于A.B之间无弹力，对A分析可以得到
，故B错；
C、细线剪断的瞬间，弹簧的弹力不变，故C错；
D、剪断细线瞬间，对A.B系统，加速度：
，故D对；
故选D
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
