题目内容
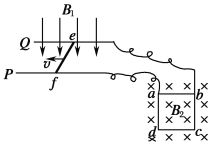
【题目】如图所示,P、Q为水平面内平行放置的光滑金属长直导轨,间距为L1,处在竖直向下、磁感应强度大小为B1的匀强磁场中.一导体杆ef垂直于P、Q放在导轨上,在外力作用下向左做匀速直线运动.质量为m、每边电阻均为r、边长为L2的正方形金属框abcd置于竖直平面内,两顶点a、b通过细导线与导轨相连,磁感应强度大小为B2的匀强磁场垂直金属框向里,金属框恰好处于静止状态.不计其余电阻和细导线对a、b点的作用力.
(1)通过ab边的电流Iab是多大?
(2)导体杆ef的运动速度v是多大?
【答案】(1)![]() (2)
(2)![]()
【解析】
外电路是ad、dc、cb三边电阻串联后再与ab边电阻并联构成,竖直方向上ab边与cd边所受安培力均向上,根据受力平衡列方程即可求解,注意并联电路中电流与电阻关系;根据闭合电路欧姆定律求出电源的电动势,根据E=BLv,即可求出导体棒的速度。
(1)设通过正方形金属框的总电流为I,ab边的电流为Iab,dc边的电流为Idc,有
![]()
![]()
金属框受重力和安培力,处于静止状态,有mg=B2IabL2+B2IdcL2
联立以上解得:![]()
(2)由(1)可得![]()
设导体杆切割磁感线产生的电动势为E,有E=B1L1v
设ad、dc、cb三边电阻串联后与ab边电阻并联的总电阻为R,则![]()
根据闭合电路欧姆定律,有![]()
联立以上解得:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目