��Ŀ����
����Ŀ����ͼ��ʾ,�����Ϊ30����б���Ϲ̶�һ���費�ƵĹ⻬ƽ�н�������,���ΪL,�¶˽�����ֵΪR�ĵ���,���촦����ǿ�ų���,�Ÿ�Ӧǿ�ȴ�СΪB,������б�洹ֱ(ͼ��δ���),����Ϊm�����費�ƵĽ�����ab��̶���б���Ϸ��ľ�Ե��������,���ɴ���ԭ�������������ֽ�������������ɾ�ֹ��ʼ�����˶�����x�������λ��,�˹����н�����ʼ���뵼�촹ֱ���������ýӴ�,����ʼ���ڵ�������,�������ٶ�Ϊg���� ��
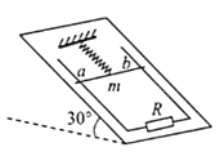
A. ��ʼ�˶�ʱ�������ļ��ٶ�С��g/2
B. ���������ٶ�Ϊvʱ,���ܵİ�����![]()
C. �˹�����,ͨ������R���ܵ����Ϊ![]()
D. �˹��̵ļ��ٽ�,��·�еĽ�����С�ڽ������������ܵļ���
���𰸡�D
��������
A����ʼ�˶�ʱ��������ֻ�ܵ������ͽ�������Խ�����ab��֧����������ţ�ٵڶ����ɿɵý������ļ��ٶ�Ϊ![]() ����ѡ��A����
����ѡ��A����
B�����������ٶ�Ϊ![]() ʱ���������и�Ÿ��߲����ĸ�Ӧ�綯��
ʱ���������и�Ÿ��߲����ĸ�Ӧ�綯��![]() �����ܵİ�����
�����ܵİ�����![]() ����ѡ��B����
����ѡ��B����
C���˹����У�ͨ������R���ܵ����Ϊ![]() ����ѡ��C����
����ѡ��C����
D������ٶ�ʱ��������б��ķ������ڵ��ɵĵ����Ͱ�����֮�ͣ�֮����ٽ��а�������С����������б��ķ������䣬���������������ڿ˷����������������л�·�еĽ�����С�ڽ������������ܵļ��٣���ѡ��D��ȷ��