题目内容
11. 如图所示,两根刚性轻杆上端由自由旋转轴A连接,轻杆下端固定一根自然伸长的匀质轻弹簧,围成边长为L的等边三角形ABC,将此装置竖直放在光滑水平面上,在轴A处施加竖直向下的大小为F的作用力,弹簧被拉伸一定长度,若此时弹簧弹力大小恰为$\frac{F}{2}$,则弹簧的劲度系数为( )
如图所示,两根刚性轻杆上端由自由旋转轴A连接,轻杆下端固定一根自然伸长的匀质轻弹簧,围成边长为L的等边三角形ABC,将此装置竖直放在光滑水平面上,在轴A处施加竖直向下的大小为F的作用力,弹簧被拉伸一定长度,若此时弹簧弹力大小恰为$\frac{F}{2}$,则弹簧的劲度系数为( )| A. | $\frac{F}{(\sqrt{2}-1)L}$ | B. | $\frac{F}{2(\sqrt{2}-1)L}$ | C. | $\frac{F}{(\sqrt{5}-1)L}$ | D. | $\frac{F}{2(\sqrt{5}-1)L}$ |
分析 先对整体受力分析,明确两端点受支持力,再由力的合成及几何关系可求得弹簧的形变量;则可由胡克定律求得劲度系数.
解答 解:对整体分析可知,整体受压力和支持力的作用,则可知,BC两杆的端点受地面向上的大小为$\frac{F}{2}$的弹力;
因弹簧的弹力也为$\frac{F}{2}$,根据三力平衡可知,此时杆与地面间的夹角为45°;则由几何关系可知,此时弹簧的长度以为$\sqrt{2}$L;则其形变量为:($\sqrt{2}$L-L);则由胡克定律可得:k=$\frac{\frac{F}{2}}{2L-L}$=$\frac{F}{2(\sqrt{2}-1)L}$;
故选:B.
点评 本题考查共点力平衡条件的应用,要注意明确杆及弹簧均不计重力,故只考虑外力即可分析.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.LC回路中电容器两端电压U随时间t变化的关系如图所示,则( )
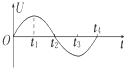

| A. | 在时刻t2,电路中的电流为零 | |
| B. | 在时刻t3,电路中的磁场能最大 | |
| C. | 从时刻t2至t3,电路中的电场能不断增大 | |
| D. | 从时刻t3至t4,电容器所带的电荷量不断增大 |
19.假设地球是一半径为R,质量分布均匀的球体.假设一矿井深度为d=$\frac{R}{2}$,已知质量分布均匀的球壳对壳内物体的引力为零.矿井底部和地面处的重力加速度大小之比为( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 2 | D. | $\frac{1}{2}$ |
16.关于永动机和热力学定律的讨论,系列叙述正确的是 ( )
| A. | 第二类永动机违反能量守恒定律 | |
| B. | 热量不可能自发地从低温物体传到高温物体 | |
| C. | 对某物体做功,物体的内能必定增加 | |
| D. | 可以从单一热源吸收热量,使之完全变为功 | |
| E. | 能量耗散从能量转化角度反映出自然界中的宏观过程具有方向性 |
3.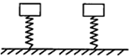 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )| A. | 两物块达最大速度时的高度相同 | B. | 上升的最大高度不同 | ||
| C. | 最大加速度相同 | D. | 最大重力势能不同 |
20.如图所示,两束单色光a,b射向水面A点,经折射后组成一束复色光,则( )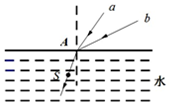

| A. | 在水中a光的速度比b光的速度小 | |
| B. | 以水下S点为光源向水面发射复色光,a光更容易发生全反射 | |
| C. | 用同一双缝干涉实验装置做实验,a光的干涉条纹间距大于b光的间距 | |
| D. | 若a、b两束光的入射角均增加相同角度,经水的折射后仍能组成一束复色光 |

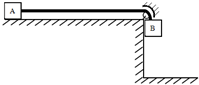 如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求:
如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求: