题目内容

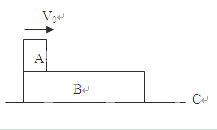
如图所示，一质量为m的滑块从高为h的光滑圆弧形槽的顶端A处无初速度地滑下，圆弧的半径为R, 槽的底端B与水平传A带相接，传送带的运行速度为v0，长为L,滑块滑到传送带上后做匀加速运动，滑到传送带右端C时，恰好被加速到与传送带的速度相同，求：?

(1)滑块到达底端B时对轨道的压力F?
(2)滑块与传送带间的动摩擦因数μ??
(3)此过程（即滑块在传送带上运动）的时间
（1）（2）（3）t=2L/(v0+)

试题分析：(1)设滑块到达B点的速度为v，由机械能守恒定律，有
.     F-mg=mv2/R   
(2)滑块在传送带上做匀加速运动，受到传送带对它的滑动摩擦力，有μmg =ma,滑块对地位移为L，末速度为v0，则，得
(3)  t=2L/(v0+)   2分
点评：本题中涉及到空间量：高度h和距离L，优先考虑运用动能定理研究．比较容易．
练习册系列答案
相关题目
如图所示，质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳，最终落入水中。若忽略运动员的身高。取g=10m/s2，求：

（1）运动员在跳台上时具有的重力势能（以水面为参考平面）；
（2）运动员起跳时的动能；
（3）运动员入水时的速度大小。
如图所示，静置于水平地面的三辆手推车沿一直线排列，质量均为m，人在极短的时间内给第一辆车一水平冲量使其运动，当车运动了距离L时与第二辆车相碰，两车以共同速度继续运动了距离L时与第三车相碰，三车以共同速度又运动了距离L时停止。车运动时受到的摩擦阻力恒为车所受重力的k倍，重力加速度为g，若车与车之间仅在碰撞时发生相互作用，碰撞时间很短，忽略空气阻力，求：

（1）整个过程中摩擦阻力所做的总功；
（2）人给第一辆车水平冲量的大小；
质量为m的物体，受到恒定阻力，在距地面h高处以 的加速度由静止竖直下落到地面，下列说法中正确的是(   )
A．物体重力势能减少B．物体克服阻力做功
C．物体的动能增加D．重力做功mgh
一个质量为m的小铁块沿半径为R的固定半圆轨道上边缘由静止滑下，到半圆底部时，小铁块所受向心力为铁块重力的1.5倍，则此过程中铁块损失的机械能为 (     )
A．B．C．D．
(10分) 一架喷气式飞机，质量m=5×103kg，起飞过程中从静止开始滑跑的路程为s =5.3×102m时，达到起飞的速度v =60m/s，在此过程中飞机受到的平均阻力是飞机重量的0.02倍（k=0.02），求飞机受到的牵引力.（结果保留两位有效数字）
如图，质量为m的小铁块A以水平速度V0冲上质量为M，长度为l，置于光滑水平面C上的木板B，正好不从木块板上掉下，已知A、B间的动摩擦因数为u，此时长木板对地位移为S，求这一过程中：

（1）、木板增加的动能
（2）、小铁块减少的动能
（3）、系统机械能的减少量
（4）、系统产生的热量
如图甲所示，水平桌面的左端固定一竖直放置的光滑圆弧轨道，其半径R=0.5m，圆弧轨道底端与水平桌面相切于C点，桌面CD长L=1m，高h2=0.5m，有质量为m（m为未知）的小物块从圆弧上A点由静止释放，A点距桌面的高度h1=0.2m，小物块经过圆弧轨道底端滑到桌面CD上，在桌面CD上运动时始终受到一个水平向右的恒力F作用。然后从D点飞出做平抛运动，最后落到水平地面上。设小物块从D点飞落到水平地面上的水平距离为x，如图乙是x2—F的图象，取重力加速度g=10m/s2。

（1）试写出小物块经D点时的速度vD与x的关系表达式。
（2）小物块与水平桌面CD间动摩擦因数μ是多少？
（3）若小物块与水平桌面CD间动摩擦因数μ是从第（2）问中的值开始由C到D均匀减小，且在D点恰好减小为0。再将小物块从A由静止释放，经过D点滑出后的水平位移大小为1m，求此情况下的恒力F的大小。
（10分）如图，水平面上O点右侧空间有一匀强电场，场强大小E =，方向水平向右，在O处放一个质量为m=0.1kg、带电量的绝缘物块，它与水平面之间的动摩擦因数μ=0.2。现给物块一个水平向右的初速度，(已知物块与水平面间的最大静摩擦力等于其滑动摩擦力，g取10m/s2)求:

（1）物块第一次速度为零时，该点与O点电势差的大小
（2）物块最终停止时，该点与O点的水平距离。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网