题目内容
（14分）如图所示，竖直平面内有两光滑金属圆轨道，平行正对放置，直径均为d，电阻不计。某金属棒长L、质量m、电阻r，放在圆轨道最低点MM' 处，与两导轨刚好接触。两圆轨道通过导线与电阻R相连。空间有竖直向上的匀强磁场，磁感应强度为B。现使金属棒获得垂直纸面向里的初速度vo，当其沿圆轨道滑到最高点NN' 处时，对轨道恰无压力（滑动过程中金属棒与圆轨道始终接触良好）。重力加速度为g，求：
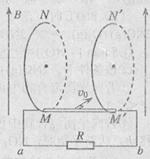
（1）金属棒刚获得垂直纸面向里的初速度时，判断电阻R中电流的方向；
（2）金属棒到达最高点NN' 处时，电路中的电功率；
（3）金属棒从MM' 处滑到NN' 处的过程中，电阻R上产生的焦耳热。
（1）金属棒刚获得垂直纸面向里的初速度时，判断电阻R中电流的方向；
（2）金属棒到达最高点NN' 处时，电路中的电功率；
（3）金属棒从MM' 处滑到NN' 处的过程中，电阻R上产生的焦耳热。
（1）由右手定则可判定R中电流方向从b到a （2） 
（3）QR=
（
mv
－ 
mgd）
（3）QR=（mv－ mgd）（1）由右手定则可判定R中电流方向从b到a（2分）
（2）设金属棒到达最高点NN′处时，速度大小为v，由牛顿第二定律得 mg =
（2分）∴ v =
E = BLv （2分）
P =
（2分）∴ P =
（1分）（3）设整个电路中产生的焦耳热为Q，则由能量守恒定律得Q=
mv－(mv2+mgd) （2分）又由Q=I2Rt 可知R中的焦耳热为QR=
（2分）即QR=
（mv－ mgd）（1分）
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
，两金属板间电压
；在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域，正三角形ABC内存在垂直纸面向里的匀强磁场Bl，三角形的上顶点A与上金属板M平齐，BC边与金属板平行，AB边的中点P恰好在下金属板N的右端点；正三角形FGH内存在垂直纸面向外的匀强磁场B2，已知A、F、G处于同一直线上，B、C、H也处于同一直线上，AF两点距离为
。现从平行金属极板MN左端沿中轴线方向入射一个重力不计的带电粒子，粒子质量
，带电量
，初速度
。
。一质量为m、电荷量为+q的带电小环穿在轨道内，它与两根直轨道间的动摩擦因数为μ（0<μ<1），而轨道的圆弧形部分均光滑。将小环在较长的直轨道CD下端的C点无初速释放（不考虑电场和磁场的边界效应，重力加速度为g），求：
，则小环在两根直轨道上通过的总路程多大？
（k为静电力常量）的正点电荷，点电荷产生的电场只存在于CD边界的右侧。今在M点释放一个质量为m、电量为-e的电子（重力不计）。求：
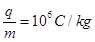的正电荷置于电场中O点由静止释放，经过
后，电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场，磁场与纸面垂直，磁感应强度B按图b所示规律周期性变化（图b中磁场以垂直纸面向外为正，以电荷第一次通过MN时为t=0时刻，忽略磁场变化带来的影响）。求：
时刻电荷与O点的竖直距离r。
圆弧导轨，O、P连线水平，M、N与E、F在同一水平高度，水平和圆弧导轨电阻不计，在其上端连有一阻值为R=8W的电阻，在PQ左侧有处于竖直向上的有界匀强磁场，磁感应强度大小为B0=6T。现有一根长度稍大于L、质量为m=0.2kg、电阻为r=2W的金属棒从轨道的顶端P处由静止开始下滑，到达轨道底端MN时对轨道的压力为2mg，取g=10m/s2，求：