题目内容
(Ⅰ)某同学设计了一个测定油漆喷枪向外喷射油漆雾滴速度的实验.他采用图1所示的装置,该油漆喷枪能够向外喷射四种速度大小不同的油漆雾滴,设喷射速度大小为v0.一个直径为D=40cm的纸带环,安放在一个可以按照一定转速转动的固定转台上,纸带环上刻有一条狭缝A,在狭缝A的正对面画一条标志线.在转台开始转动达到稳定转速时,向侧面同样开有狭缝B的纸盒中喷射油漆雾滴,当狭缝A转至与狭缝B正对平行时,雾滴便通过狭缝A在纸带的内侧面留下痕迹.改变喷射速度重复实验,在纸带上留下一系列的痕迹a、b、c、d.将纸带从转台上取下来,展开平放在刻度尺旁边,如图所示.已知v0>
,则:

(1)在上图中,速度最大的雾滴所留的痕迹是
(2)如果不计雾滴所受的空气阻力,转台转动的角速度为2.1rad/s,则该喷枪喷出的油漆雾滴速度的最大值为
(Ⅱ)有两个完全相同,但刻度盘上仅有刻度而没有标度值的电压表,电压表的内阻约为5000Ω.现打算用图(1)所示的电路测量它们的内阻,其中E为电动势12V、内阻可忽略不计的电源,R1是调节范围为0~9999Ω的电阻箱;R2是调节范围为0~1000Ω的滑动变阻器;S为电键.

①闭合电键S之前,滑动变阻器的滑片P应滑到变阻器的
②闭合电键之后,适当调节滑动变阻器滑片P和电阻箱的旋钮,当电阻箱调节成图(2)所示的情景时,两电压表指针的位置如图(3)所示,由此可知,此时电阻箱的阻值为
| ω?D | π |

(1)在上图中,速度最大的雾滴所留的痕迹是
d
d
点,该点到标志线的距离为0.70
0.70
cm.(2)如果不计雾滴所受的空气阻力,转台转动的角速度为2.1rad/s,则该喷枪喷出的油漆雾滴速度的最大值为
24
24
m/s;考虑到空气阻力的影响,该测量值小于
小于
真实值(选填“大于”、“小于”或“等于”).(Ⅱ)有两个完全相同,但刻度盘上仅有刻度而没有标度值的电压表,电压表的内阻约为5000Ω.现打算用图(1)所示的电路测量它们的内阻,其中E为电动势12V、内阻可忽略不计的电源,R1是调节范围为0~9999Ω的电阻箱;R2是调节范围为0~1000Ω的滑动变阻器;S为电键.

①闭合电键S之前,滑动变阻器的滑片P应滑到变阻器的
a
a
端.(填“a”或“b”).②闭合电键之后,适当调节滑动变阻器滑片P和电阻箱的旋钮,当电阻箱调节成图(2)所示的情景时,两电压表指针的位置如图(3)所示,由此可知,此时电阻箱的阻值为
2547
2547
Ω,这两个电压表的内阻均为5094
5094
Ω.分析:Ⅰ、(1)油漆雾滴进入狭缝A后沿直线匀速运动到纸带环上,若纸带环不转,则油漆雾滴一定打在标志线上,若纸带环以某一角速度转动,则油漆雾滴沿直线到达纸带环时,标志线在油漆雾滴运动到纸带环上的这段时间内会转过一定角度θ;v0>
,故雾滴飞到纸带时间内,转过的角度小于π,即转动小于半圈;雾滴运动的路程一定,速度越大,运行的时间越短,此时转台转过的弧度越小,打在纸带上的点距离标志线的距离越小.
(2)在纸带环转速ω一定的情况下,油漆雾滴速度越大,到达纸带环的时间t越短,则标志线转过的角度θ越小,转过的弧长s越短,油漆雾滴到达纸带环的位置距离标志线越近,所以到达d点的油漆雾滴是速度最大的.
Ⅱ、为保护电路,连接电路时,应断开开关,滑动变阻器接入电路的阻值应为最大阻值.
根据电阻箱上的显示可读出阻值,根据两表示数关系结合欧姆定律,可判断电压表的电阻是电阻箱所示阻值的关系去求解.
| ω?D |
| π |
(2)在纸带环转速ω一定的情况下,油漆雾滴速度越大,到达纸带环的时间t越短,则标志线转过的角度θ越小,转过的弧长s越短,油漆雾滴到达纸带环的位置距离标志线越近,所以到达d点的油漆雾滴是速度最大的.
Ⅱ、为保护电路,连接电路时,应断开开关,滑动变阻器接入电路的阻值应为最大阻值.
根据电阻箱上的显示可读出阻值,根据两表示数关系结合欧姆定律,可判断电压表的电阻是电阻箱所示阻值的关系去求解.
解答:解:Ⅰ(1)转盘的角速度一定,雾滴速度越大,运行时间越短,在雾滴运行的时间内,转盘转过的角度越小,故雾滴与标志线的距离越近;
故d点对应雾滴的速度最大,毫米刻度尺读数要估读,为0.70mm;
故答案为:d,0.70;
(2)速度最大的是d点,距离标志线的距离是△S=0.70cm,根据
t=
=
△S=
△θ
解得:v0=
=24m/s.
若考虑空气阻力,实际上雾滴做减速运动,现在将雾滴当做匀速直线运动的计算,求出来的速度要小于真实的速度.
Ⅱ①为保护电路,连接电路时,应断开开关,滑动变阻器接入电路的阻值应为最大阻值,即滑到a端.
②从电阻箱读出的阻值为R=2547Ω,
根据欧姆定律得:I=
从两电压表指针的位置可知,与电阻箱串联的电压的电流与另一电压表中的电流比值为2:3,
根据电压相等可得电压表的电阻是电阻箱所示阻值的两倍.
所以电压表的内阻:RV=5094Ω;
故答案为:(Ⅰ)(1)d,0.70,(2)24,小于
(Ⅱ)①a
②2547,5094
故d点对应雾滴的速度最大,毫米刻度尺读数要估读,为0.70mm;
故答案为:d,0.70;
(2)速度最大的是d点,距离标志线的距离是△S=0.70cm,根据
t=
| D |
| v0 |
| △θ |
| ω |
△S=
| D |
| 2 |
解得:v0=
| Dω |
| △θ |
若考虑空气阻力,实际上雾滴做减速运动,现在将雾滴当做匀速直线运动的计算,求出来的速度要小于真实的速度.
Ⅱ①为保护电路,连接电路时,应断开开关,滑动变阻器接入电路的阻值应为最大阻值,即滑到a端.
②从电阻箱读出的阻值为R=2547Ω,
根据欧姆定律得:I=
| U |
| RV |
从两电压表指针的位置可知,与电阻箱串联的电压的电流与另一电压表中的电流比值为2:3,
根据电压相等可得电压表的电阻是电阻箱所示阻值的两倍.
所以电压表的内阻:RV=5094Ω;
故答案为:(Ⅰ)(1)d,0.70,(2)24,小于
(Ⅱ)①a
②2547,5094
点评:1、本题关键要明确雾滴的运动是匀速直线运动,纸盘是匀速圆周运动,两者同时运行,但互不影响.
2、本题考查了滑动变阻器的作用以及串并联、欧姆定律的应用.,
2、本题考查了滑动变阻器的作用以及串并联、欧姆定律的应用.,

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目

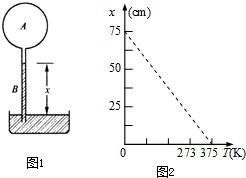 某同学设计了一种测温装置,其结构如图1所示,玻璃泡A内封有一定质量的气体,与A相连的细管B插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出,设B管的体积与A泡的体积相比可略去不计.
某同学设计了一种测温装置,其结构如图1所示,玻璃泡A内封有一定质量的气体,与A相连的细管B插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出,设B管的体积与A泡的体积相比可略去不计.
 (2011?重庆一模)某同学设计了一种测定风力、风速的装置,其原理如图所示,迎风板与一轻弹簧的一端N相接,一起穿在光滑的金属杆上.弹簧是绝缘材料制成的,其劲度系数k=1300N/m,自然长度L0=0.5m,均匀金属杆用电阻率较大的合金制成,迎风板面积为S=0.5m2,工作时总是正对着风吹来的方向.电路中左端导线与金属杆M端固定相连,右端导线接在N点并可随迎风板在金属杆上滑动,且与金属杆接触良好.限流电阻的阻值R=1.0Ω,电源电动势E=12.0V,内阻r=0.5Ω.合上开关,没有风吹时,弹簧处于原长,理想电压表的示数U1=3.0V.求:
(2011?重庆一模)某同学设计了一种测定风力、风速的装置,其原理如图所示,迎风板与一轻弹簧的一端N相接,一起穿在光滑的金属杆上.弹簧是绝缘材料制成的,其劲度系数k=1300N/m,自然长度L0=0.5m,均匀金属杆用电阻率较大的合金制成,迎风板面积为S=0.5m2,工作时总是正对着风吹来的方向.电路中左端导线与金属杆M端固定相连,右端导线接在N点并可随迎风板在金属杆上滑动,且与金属杆接触良好.限流电阻的阻值R=1.0Ω,电源电动势E=12.0V,内阻r=0.5Ω.合上开关,没有风吹时,弹簧处于原长,理想电压表的示数U1=3.0V.求: