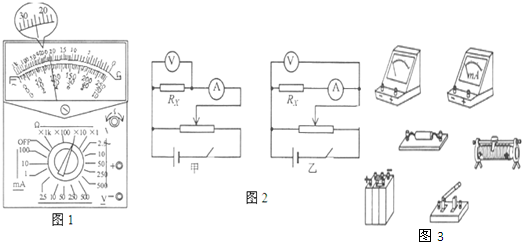
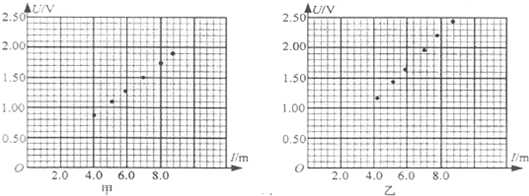
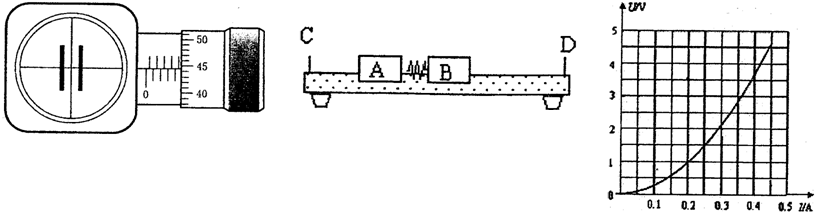
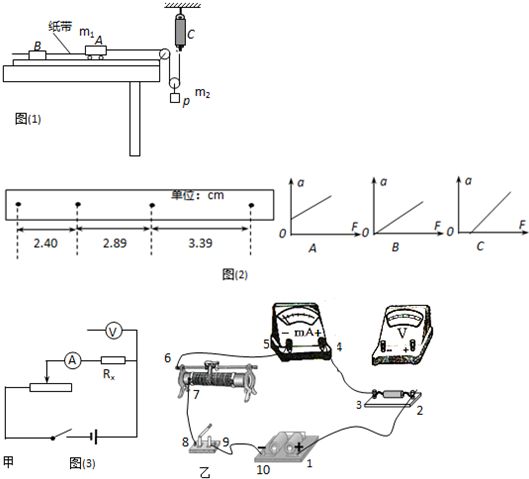
题目内容
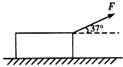 如图所示,质量为5kg的物体与水平地面间的动摩擦因数μ=0.2,现用F=25N、与水平方向成θ=37°的力拉物体,使物体从静止开始做匀加速运动,求:
如图所示,质量为5kg的物体与水平地面间的动摩擦因数μ=0.2,现用F=25N、与水平方向成θ=37°的力拉物体,使物体从静止开始做匀加速运动,求:(1)物体加速度的大小;
(2)物体在第2秒内的位移.(g取10m/s2,sin37=0.6,cos37=0.8)
分析:建立直角坐标系对物体进行受力分析,由题意知物体在水平方向所受的合力产生加速度,竖直方向所受合力为0,分别列牛顿第二定律和平衡方程求解出加速度,根据加速度由运动学公式求物体在第2秒内产生的位移.
解答:解:(1)建立如图的直角坐标系,对物体进行受力分析有:
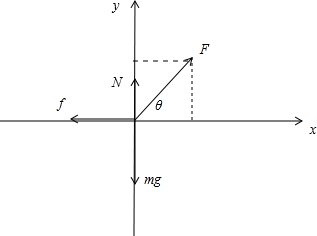
据牛顿第二定律有:
F合x=Fcosθ-f=ma ①
F合y=N+Fsinθ-mg=0 ②
又滑动摩擦力f=μN ③
由①②③式可得:
a=
代入数据可得物体产生的加速度a=2.6m/s2
(2)因为物体做初速度为0的匀加速直线运动,根据位移时间关系x=
at2有:
物体在第1s内的位移x1=
×2.6×12m=1.3m
物体在前2s内的位移x2=
×2.6×22m=5.2m
所以物体在第2s内的位移x=x2-x1=5.2-1.3m=3.9m
答:(1)物体产生的加速度大小为2.6m/s2;
(2)物体在第2s内的位移为3.9m.

据牛顿第二定律有:
F合x=Fcosθ-f=ma ①
F合y=N+Fsinθ-mg=0 ②
又滑动摩擦力f=μN ③
由①②③式可得:
a=
| Fcosθ-μ(mg-Fsinθ) |
| m |
代入数据可得物体产生的加速度a=2.6m/s2
(2)因为物体做初速度为0的匀加速直线运动,根据位移时间关系x=
| 1 |
| 2 |
物体在第1s内的位移x1=
| 1 |
| 2 |
物体在前2s内的位移x2=
| 1 |
| 2 |
所以物体在第2s内的位移x=x2-x1=5.2-1.3m=3.9m
答:(1)物体产生的加速度大小为2.6m/s2;
(2)物体在第2s内的位移为3.9m.
点评:本题求加速度时易出错的地方就是求摩擦力时,物体与地面间的弹力不等于物体的重力,求第2s内位移时易当成前2s内位移求解,解题要注意.

练习册系列答案
相关题目


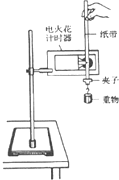 (1)如图所示,将电火花计时器固定在铁架台上,使重物带动纸带从静止开始自由下落,利用此装置可以测定重力加速度.
(1)如图所示,将电火花计时器固定在铁架台上,使重物带动纸带从静止开始自由下落,利用此装置可以测定重力加速度.