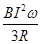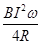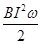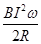题目内容
如图所示,均匀金属环的电阻为R,其圆心O,半径为L。一金属杆OA,质量可忽略不计,电阻为r,可绕O点转动,A端固定一质量为m的金属球a,球上有孔,套在圆环上可无摩擦滑动,Ob为一导线,整个装置放在与环平面垂直的匀强磁场中,磁感应强度为B。现把金属杆OA从水平位置由静止释放运动到竖直位置,球a的速度为v,则OA到竖直位置时产生的电动势为________;此时OA所受安培力的功率为________;杆OA由水平位置转到竖直位置这段时间内,电路中转化的内能为________。

【答案】
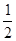 BLυ
—
BLυ
—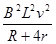 mgL-
mgL-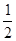 mυ2
mυ2
【解析】
试题分析:OA的转动切割磁感线,求运动到最低点时的瞬时电动势和瞬时功率,应用法拉第电磁感应定律时,要运用旋转切割的情况。最后要求的是过程量,应用能量的转化和守恒。
解:根据金属杆旋转切割产生的感应电动势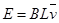 ,因为在金属杆上
,因为在金属杆上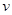 随L均匀变化,所以
随L均匀变化,所以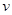 可以用始末位置的平均值,所以
可以用始末位置的平均值,所以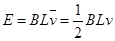 。
。
根据功能关系可知克服安培力的功率等于整个电路消耗的电功率: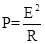 ,外电路为并联电路,与内阻r串联,所以总电阻R=
,外电路为并联电路,与内阻r串联,所以总电阻R=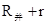 =
=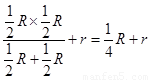 ,
,
将E,r代入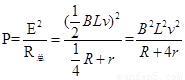
所以安培力的功率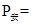 —
—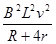
根据能量的转化与守恒Q= mgL-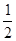 mυ2
mυ2
考点:感应电动势 功能关系 能量的转化与守恒
点评:该题为一个难题,考查的知识点较多。掌握旋转切割求电动势时注意用平均速度。求解安培力的功率时,注意应用功能关系,克服安培力做多少功,整个电路就生成多少电能。

练习册系列答案
相关题目
 如图所示,均匀金属圆环总电阻为2R,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为l,电阻为
如图所示,均匀金属圆环总电阻为2R,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为l,电阻为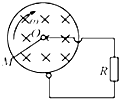 如图所示,均匀金属圆环电阻不计,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为L,电阻为
如图所示,均匀金属圆环电阻不计,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为L,电阻为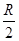 ,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是
,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是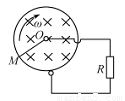

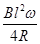
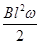
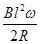
 ,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是( )
,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是( )