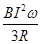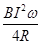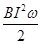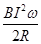题目内容
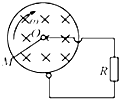 如图所示,均匀金属圆环电阻不计,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为L,电阻为
如图所示,均匀金属圆环电阻不计,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为L,电阻为| R | 2 |
(1)求金属杆OM两端的电势差UOM
(2)电阻R消耗的电功率.
分析:(1)金属杆OM转动切割磁感线产生的感应电动势,由公式E=BLv,v是平均速度求出,再根据闭合电路欧姆定律,求出回路中的电流强度I,金属杆OM两端的电势差UOM
等于路端电压,就是R两端的电压,由欧姆定律求解.运用右手定则判断OM电势的高低.
(2)电阻R消耗的功率为:P=I2R.
等于路端电压,就是R两端的电压,由欧姆定律求解.运用右手定则判断OM电势的高低.
(2)电阻R消耗的功率为:P=I2R.
解答:解:(1)根据法拉第电磁感应定律,金属杆切割磁感线,产生的感应电动势为:
E=BL
=BL
=
BL2ω
根据闭合电路欧姆定律,回路中电流强度为:
I=
金属杆OM两端的电势差即为电阻R两端的电压U
U=IR
由右手定则可知,O点电势比M点电势低
则 UOM=-
BL2ω
(2)电阻R消耗的功率为:P=I2R
解得:P=
答:
(1)金属杆OM两端的电势差UOM为-
BL2ω.
(2)电阻R消耗的电功率为
.
E=BL
. |
| v |
| 0+Lω |
| 2 |
| 1 |
| 2 |
根据闭合电路欧姆定律,回路中电流强度为:
I=
| E | ||
R+
|
金属杆OM两端的电势差即为电阻R两端的电压U
U=IR
由右手定则可知,O点电势比M点电势低
则 UOM=-
| 1 |
| 3 |
(2)电阻R消耗的功率为:P=I2R
解得:P=
| B2L4ω 2 |
| 9R |
答:
(1)金属杆OM两端的电势差UOM为-
| 1 |
| 3 |
(2)电阻R消耗的电功率为
| B2L4ω 2 |
| 9R |
点评:本题考查了法拉第电磁感应定律应用的延伸情况,转动切割磁感线时E=
BL2ω对于结果要记忆.对于电势差,要注意与电压的区别,会根据右手定则判断出电势的高低,确定出电势差的正负.
| 1 |
| 2 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图所示,均匀金属圆环总电阻为2R,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为l,电阻为
如图所示,均匀金属圆环总电阻为2R,磁感应强度为B的匀强磁场垂直穿过圆环.金属杆OM长为l,电阻为 如图所示,均匀金属圆环轨道上,有一金属细杆过圆心且与环光滑相接,接点分别为A和B,杆绕过环心O且垂直于环面的轴做顺时针方向转动.环面左右两半的匀强磁场的磁感强度大小相等,都是0.2T,方向相反,都垂直于环面.设AB长为0.2m,电阻为0.1Ω,圆环总电阻为0.4Ω,AB杆转动的角速度ω=100rad/s.
如图所示,均匀金属圆环轨道上,有一金属细杆过圆心且与环光滑相接,接点分别为A和B,杆绕过环心O且垂直于环面的轴做顺时针方向转动.环面左右两半的匀强磁场的磁感强度大小相等,都是0.2T,方向相反,都垂直于环面.设AB长为0.2m,电阻为0.1Ω,圆环总电阻为0.4Ω,AB杆转动的角速度ω=100rad/s.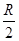 ,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是
,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是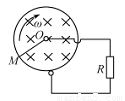

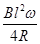
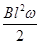
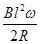
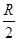 ,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是( )
,M端与环紧密接触,金属杆OM绕过圆心的转轴O以恒定的角速度ω转动,当电阻为R的一段导线一端和环连接,另一端与金属杆的转轴Ο相连接时,下列结论中正确的是( )