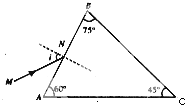
题目内容
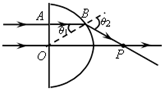
两束平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图所示.已知光线1沿直线穿过玻璃,它的入射点是O;光线2的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃截面的圆半径为R,OA=
,OP=
R,光在真空中的传播速度为c.据此可知( )
| R |
| 2 |
| 3 |
| A.光线2在圆弧面的入射角为45° | ||||
B.玻璃材料的折射率为
| ||||
C.光线1在玻璃中传播速度为
| ||||
D.光线1在玻璃中传播时间为
|

A、光线AB沿直线进入玻璃,在半圆面上的入射点为B,入射角设为θ1,折射角设为θ2,则根据几何关系得:
sinθ1=
=
=
,则入射角θ1=30°.故A错误.
B、因OP=
R,由数学上余弦定理得 BP=
=
R,而OB=R
解得:BP=R
则知 OB=BP,所以折射角 θ2=2×30°=60°
由折射定律得玻璃的折射率为:n=
=
=
.故B正确.
C、该光线在玻璃中传播速度为:v=
=
.故C错误.
D、光线在玻璃中传播时间为:t=
=
=
.故D错误.
故选:B
sinθ1=
| OA |
| OB |
| ||
| R |
| 1 |
| 2 |
B、因OP=
| 3 |
| (OB)2+(OP)-2?OB?OPcos30° |
| 3 |
解得:BP=R
则知 OB=BP,所以折射角 θ2=2×30°=60°
由折射定律得玻璃的折射率为:n=
| sinθ1 |
| sinθ2 |
| sin60° |
| sin30° |
| 3 |
C、该光线在玻璃中传播速度为:v=
| c |
| n |
| c | ||
|
D、光线在玻璃中传播时间为:t=
| AB |
| v |
| ||||
|
| 3R |
| 2c |
故选:B

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目