题目内容
如图所示，圆形区域内有垂直纸面的匀强磁场，两个质量和电荷量都相同的带电粒子a、 b，以不同的速率沿着A0方向对准圆心O射入磁场，其运动轨迹如图。若带电粒子只受磁场力的作用，则下列说法正确的是
| A．a粒子速率较大 |
| B．b粒子速率较大 |
| C．b粒子在磁场中运动时间较长 |
| D．a、b粒子在磁场中运动时间一样长 |
B
解析试题分析：带电粒子沿半径方向垂直进入圆形匀强磁场区域，离开磁场的速度也必然沿圆形磁场的半径方向，据此作出ab粒子离开磁场时的速度如图。那么圆形磁场区域和粒子圆周运动的轨迹就有一条公共弦，弦的垂直平分线过两个圆的圆心。而这条垂直平分线也是入射速度和末速度夹角的角平分线，那么这条角平分线与进磁场时垂线的交点即圆心，据此判断如下图，a粒子半径小，根据洛伦兹力提供向心力
，得
，所以a粒子速率较小，选项A错B对。带电粒子在匀强磁场中做匀速圆周运动的周期
可知两个粒子圆周运动周期相同，但是据图可知，a粒子速度偏转角大，即圆心角大，所以 a粒子运动时间长，选项CD错。
考点：带电粒子在匀强磁场中的运动
处于同一平面内的两根长直导线中通有方向相反大小不同的电流，这两根导线把它们所在的平面分成a、b、c三个区域，如图所示，则磁感强度为零的区域 
| A．可能出现在a区 | B．可能出现在b区 |
| C．可能出现在c区 | D．a区、b区、c区都有可能 |
如图所示，一半径为R的圆形区域内有垂直于纸面向里的匀强磁场，一质量为
，电量为
的正电荷（重力忽略不计）以速度
沿正对着圆心o的方向射入磁场，从磁场中射出时速度方向改变了
角。磁场的磁感应强度大小为
A． | B． |
C． | D． |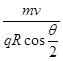
如图所示，回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电源两极相连接的两个D形金属盒，两盒间的狭缝中形成周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，D形盒半径为R．用该回旋加速器加速质子（质量数为1，核电荷数为1）时，匀强磁场的磁感应强度为B，高频交流电周期为T．（粒子通过狭缝的时间忽略不计）则
| A．质子在D形盒中做匀速圆周运动的周期为2T |
B．质子被加速后的最大速度可能超过 |
| C．质子被加速后的最大速度与加速电场的电压大小无关 |
| D．不改变B和T，该回旋加速器也能用于加速α粒子（质量数为4，核电荷数为2） |
如图所示为磁场作用力演示仪中的赫姆霍兹线圈，线圈中心处挂有一根小磁针，小磁针与线圈在同一平面内，当赫姆霍兹线圈通以如图所示方向的电流时
| A．小磁针N极向里转 |
| B．小磁针N极向外转 |
| C．小磁针在纸面内向左摆动 |
| D．小磁针在纸面内向右摆动 |
如图所示，速度不同的同种带电粒子（重力不计）a、b沿半径AO方向进入一圆形匀强磁场区域，a，b两粒子的运动轨迹分别为AB和AC，则下列说法中正确的是
| A．a、b两粒子均带正电 |
| B．a粒子的速度比b粒子的速度大 |
| C．a粒子在磁场中的运动时间比b粒子长 |
| D．两粒子离开磁场时的速度反向延长线一定都过圆心O |
如图，在正方形abcd范围内，有方向垂直纸面向里的匀强磁场，两个电子以不同的速率，从a点沿ab方向垂直磁场方向射入磁场，其中甲电子从c点射出，乙电子从d点射出。不计重力，则甲、乙电子（ ）
| A．速率之比2:1 |
| B．在磁场中运行的周期之比1:2 |
| C．在正方形磁场中运行的时间之比1:2 |
| D．速度偏转角之比为1:2 |
如图所示，三根通电长直导线P、Q、R互相平行，垂直纸面放置，其间距均为L，电流均为I，方向垂直纸面向里．已知电流为I的长直导线产生的磁场中，距导线r处的磁感应强度B=kI/r，其中k为常量．某时刻有一电荷量为q的带正电粒子经过原点O，速度大小为v，方向沿y轴正方向，该粒子此时所受磁场力为
A．方向垂直纸面向外，大小为 |
B．方向指向x轴正方向，大小为 |
C．方向垂直纸面向外，大小为 |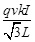
D．方向指向x轴正方向，大小为 |
如图，甲图是回旋加速器的原理示意图。其核心部分是两个D型金属盒，在加速带电粒子时，两金属盒置于匀强磁场中（磁感应强度大小恒定），并分别与高频电源相连。加速时某带电粒子的动能EK随时间t变化规律如乙图所示，若忽略带电粒子在电场中的加速时间，则下列判断正确的是 ( ) 
| A．高频电源的变化周期应该等于tn－tn-2 |
| B．在EK-t图象中t4－t3＝t3－t2＝t2－t1 |
| C．粒子加速次数越多，粒子获得的最大动能一定越大 |
| D．不同粒子获得的最大动能都相同 |