题目内容
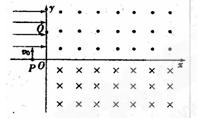
(18分)如图所示,带电平行金属板PQ和MN之间的距离为d;两金属板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B。如图建立坐标系,x轴平行于金属板,与金属板中心线重合,y轴垂直于金属板。区域I的左边界在y轴,右边界与区域II的左边界重合,且与y轴平行;区域II的左、右边界平行。在区域I和区域II内分别存在匀强磁场,磁感应强度大小均为B,区域I内的磁场垂直于Oxy平面向外,区域II内的磁场垂直于Oxy平面向里。一电子沿着x轴正向以速度v0射入平行板之间,在平行板间恰好沿着x轴正向做直线运动,并先后通过区域I和II。已知电子电量为e,质量为m,区域I和区域II沿x轴方向宽度均为 。不计电子重力。
。不计电子重力。
(1)求两金属板之间电势差U;
(2)求电子从区域II右边界射出时,射出点的纵坐标y;
(3)撤除区域I中的磁场而在其中加上沿x轴正向的匀强电场,使得该电子刚好不能从区域II的右边界飞出。求电子两次经过y轴的时间间隔t。
(1)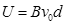 (2)
(2)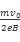 (3)
(3)
解析试题分析:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡 即
即 (2分)
(2分)
所以,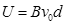 (2分)
(2分)
(2)如图所示,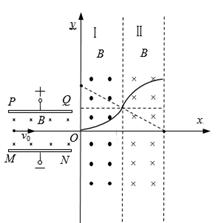
电子进入区域I做匀速圆周运动,向上偏转,洛伦兹力提供向心力 所以,
所以,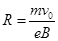 (2分)
(2分)
设电子在区域I中沿着y轴偏转距离为 y0,区域I的宽度为b(b=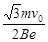 ),则
),则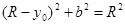 (2分)
(2分)
代入数据,解得 (1分)
(1分)
电子在两个磁场中有相同的偏转量。
电子从区域II射出点的纵坐标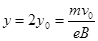 (2分)
(2分)
(3)电子刚好不能从区域II的右边界飞出,说明电子在区域II中做匀速圆周运动的轨迹恰好与区域II的右边界相切,圆半径恰好与区域II宽度相同。设电子进入区域II时的速度为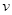 ,
,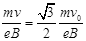 ,所以
,所以 (2分)
(2分)
电子通过区域I的过程中,向右做匀加速直线运动, 此过程中平均速度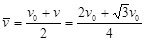
电子通过区域I的时间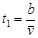 (b为区域I的宽度
(b为区域I的宽度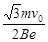 )
)
解得: 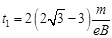 (1分)
(1分)
电子在区域II中运动了半个圆周,设电子做圆周运动的周期为T,则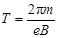
电子在区域II中运动的时间 (2分)
(2分)
电子反向通过区域I的时间仍为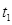 。所以, 电子两次经过y轴的时间间隔
。所以, 电子两次经过y轴的时间间隔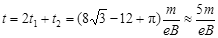 (2分)
(2分)
考点:带电粒子在磁场中运动

如图所示,竖直放置的平行金属导轨上端跨接一个阻值为R的电阻。质量为m的金属棒MN可沿平行导轨竖直下滑,不计轨道与金属棒的电阻。金属棒自由下落了 h后进入一个有上下边界的匀强磁场区域,磁场方向垂直轨道平面,磁场宽度也为h ,设金属棒MN到达上边界aa'时的速度为 ,到达下边界bb'时的速度为
,到达下边界bb'时的速度为 ,则以下说法正确的是
,则以下说法正确的是
A.进入磁场区后,MN可能做匀速运动,则 |
B.进入磁场区后,MN可能做加速运动,则 |
C.进入磁场区后,MN可能做减速运动,则 |
D.通过磁场区域的过程中,R上释放出的焦耳热一定是mg |

 和此时磁感应强度B的大小;
和此时磁感应强度B的大小; ,求此时U1与U2的比值;若使电子打在荧光屏上某点,该点距O点距离为d,只改变一个条件的情况下,请你提供一种方案,并说明理由。
,求此时U1与U2的比值;若使电子打在荧光屏上某点,该点距O点距离为d,只改变一个条件的情况下,请你提供一种方案,并说明理由。 在什么范围内,离子才能打在金属板PQ上?
在什么范围内,离子才能打在金属板PQ上?


 进入匀强电场,恰好经过y轴上的Q点且与y轴成450角射出电场,再经过一段时间又恰好垂直于X轴进入下面的磁场.已知OP之间的距离为d(不计粒子的重力)求:
进入匀强电场,恰好经过y轴上的Q点且与y轴成450角射出电场,再经过一段时间又恰好垂直于X轴进入下面的磁场.已知OP之间的距离为d(不计粒子的重力)求: