题目内容
13. 如图所示,在倾角θ=37°的斜面上,N点上方粗糙,下方光滑,一质量为m=0.3kg的物块(可视为质点)从N点上方离N距离为l=2.0m的P点由静止释放,下滑到N处开始压缩弹簧后又被弹离,物块第一次上滑最高位置离N点的距离为l1=1.6m,已知弹簧的劲度系数k=1.6N/m,g=10m/s2,(不计物体与弹簧接触瞬间能量的损失,sin37°=0.6,cos37°=0.8).求:
如图所示,在倾角θ=37°的斜面上,N点上方粗糙,下方光滑,一质量为m=0.3kg的物块(可视为质点)从N点上方离N距离为l=2.0m的P点由静止释放,下滑到N处开始压缩弹簧后又被弹离,物块第一次上滑最高位置离N点的距离为l1=1.6m,已知弹簧的劲度系数k=1.6N/m,g=10m/s2,(不计物体与弹簧接触瞬间能量的损失,sin37°=0.6,cos37°=0.8).求:(1)物块与粗糙斜面间的动摩擦因数;
(2)弹簧压缩最短时的弹性势能为EP.
(3)物块第三次上滑的最高点离N点的距离.
分析 (1)对于P下滑又返回的整个过程,对物块运用动能定理列式,即可求得动摩擦因数;
(2)对下滑的过程和压缩弹簧的过程列式,由功能关系即可求出;
(3)对于第二次从N运动到最高点的过程,运用动能定理求出第二次上滑到的高度;同理也可以求出第三次到达的最大高度.
解答 解:(1)设物体与斜面间的动摩擦因数为μ,则P下滑又返回的整个过程有:
$mg(l-{l_1})sin{37^0}-μmgcos{37^0}(l+{l_1})=0$
解得:$μ=\frac{{(l-{l_1})sinθ}}{{(l+{l_1})cosθ}}=\frac{1}{12}$
(2)弹簧压缩最大量为x,则mg(l+x)sin37°-μmgcos37°l=Ep
且${E_p}=\frac{0+kx}{2}x$
代入数据解得:x=3.4m
即:${E_P}=\frac{1}{2}K{X^2}=9.2J$
(3)设物块第二次、第三次上滑距N点的最大距离分别为l2、l3,则:
$mg({l_1}-{l_2})sin{37^0}-μmgcos{37^0}({l_1}+{l_2})=0$
解得:${l_2}=\frac{(sinθ-μcosθ)}{(sinθ+μcosθ)}{l_1}=\frac{4}{5}{l_1}$
同理可得:${l_3}=\frac{(sinθ-μcosθ)}{(sinθ+μcosθ)}{l_2}=\frac{4}{5}{l_2}={(\frac{4}{5})^2}{l_1}=1.024m$
答:(1)物块与粗糙斜面间的动摩擦因数是$\frac{1}{12}$;
(2)弹簧压缩最短时的弹性势能为9.2J.
(3)物块第三次上滑的最高点离N点的距离是1.024m.
点评 该题考查动能定理的应用以及功能关系,本题运用动能定理时,要灵活选择研究的过程,采用全程法和分段法结合往往比较简单.

 阅读快车系列答案
阅读快车系列答案| A. | 地球总是不停地绕太阳运动 | |
| B. | 地球周围存在着稠密的大气,它们不会发散到太空中去 | |
| C. | 成千上万个恒星聚集在一起,形成银河系的球状星团 | |
| D. | 很难把一块铁折断 |
 如图所示,在Oxy坐标系内,a、b、c是x轴上的三个点,将一正检验电荷Q由a点移至b点时,需克服静电力做功W;若从a点移至c点时,也需克服静电力做功W,下列说法正确的是( )
如图所示,在Oxy坐标系内,a、b、c是x轴上的三个点,将一正检验电荷Q由a点移至b点时,需克服静电力做功W;若从a点移至c点时,也需克服静电力做功W,下列说法正确的是( )| A. | a点电势高于b点电势 | |
| B. | a、b之间的电势差等于a、c之间的电势差 | |
| C. | 该电场可能是处于第Ⅳ象限某一位置的正点电荷形成的电场 | |
| D. | 该电场可能是匀强电场 |
 如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示,经△t=0.2s,波的图象如图中虚线所示,已知其波长为2m,则下述说法中正确的是( )
如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示,经△t=0.2s,波的图象如图中虚线所示,已知其波长为2m,则下述说法中正确的是( )| A. | 若波向右传播,则波的周期可能大于2s | |
| B. | 若波向左传播,则波的周期可能大于0.2s | |
| C. | 若波向左传播,则波的波速可能等于9m/s | |
| D. | 若波速是19m/s,则波向右传播 |
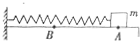 如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连.弹簧处于自然长度时物块位于O点(图中未标出).物块的质量为m,AB=x,物块与桌面间的动摩擦因数为μ.现用水平向右的力将物块从O点拉至A点,拉力做的功为W,撤去拉力后物块由静止向左运动,经O点到达B点时速度为零.重力加速度为g.则上述过程中( )
如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连.弹簧处于自然长度时物块位于O点(图中未标出).物块的质量为m,AB=x,物块与桌面间的动摩擦因数为μ.现用水平向右的力将物块从O点拉至A点,拉力做的功为W,撤去拉力后物块由静止向左运动,经O点到达B点时速度为零.重力加速度为g.则上述过程中( )| A. | 物块及弹簧组成的系统的机械能守恒 | |
| B. | 物块及弹簧组成的系统在B点的机械能小于在A点的机械能 | |
| C. | 物块在A点时,弹簧的弹性势能等于W-$\frac{1}{2}$μmgx | |
| D. | 物块在B点时,弹簧的弹性势能小于W-$\frac{3}{2}$μmgx |
 一质量m=0.5kg的滑块以一定的初速度从底端冲上一倾角为30°足够长的固定斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,并通过计算机绘制出滑块上滑过程的v-t图象,如图所示.(g取10m/s2)
一质量m=0.5kg的滑块以一定的初速度从底端冲上一倾角为30°足够长的固定斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,并通过计算机绘制出滑块上滑过程的v-t图象,如图所示.(g取10m/s2)