题目内容
5.在Oxy平面内的OPMN区域内,存在两个场强大小均为E、方向分别水平向左和竖直向上的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形.两电场之间存在一段宽为L的真空区域.已知电子的质量为m,电荷量为e,不计电子所受重力.在该区域OP边的中点处由静止释放电子,求:
(1)电子进入Ⅱ区域时的速度大小;
(2)电子从MN边离开OPMN区域时的侧移距离.
分析 (1)由动能定理可求得粒子进入II区时的速度大小;
(2)粒子在II区域中做类平抛运动,由运动的合成和分解可求得侧移距离.
解答 解:(1)设电子进入II区域时的速度为v0,由题设条件,根据动能定理可得:
$eEL=\frac{1}{2}m{v_0}^2$
解得:${v_0}=\sqrt{\frac{2eEL}{m}}$
(2)电子在I区域内做匀加速直线运动,中间区域匀速直线运动,而进入II区域做类平抛运动.在II区域内,由类平抛运动规律可得:
在水平方向上:L=v0t
在竖直方向上:$y=\frac{1}{2}a{t^2}=\frac{1}{2}\frac{eE}{m}{t^2}$
解得:$y=\frac{L}{4}$
答:(1)电子进入Ⅱ区域时的速度大小为$\sqrt{\frac{2eEL}{m}}$
(2)电子从MN边离开OPMN区域时的侧移距离为$\frac{L}{4}$
点评 本题考查带电粒子在电场中的运动,要注意对应偏转应用类平抛运动规律,对于加速可直接应用动能定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列说法正确的是( )
| A. | 太阳辐射的能量主要来自太阳内部的轻核聚变 | |
| B. | 原子核的比结合能越大表示该原子核越不稳定 | |
| C. | 轻核聚变与重核裂变均释放能量 | |
| D. | 放射性元素衰变的快慢只由核内部自身的因素决定 | |
| E. | 实验表明,只要照射光的强度足够大,就一定能发生光电效应现象 |
16. 如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )
如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )
 如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )
如图,地面上某空间区域内,水平虚线上方存在场强为E1、方向竖直向下的匀强电场,虚线下方存在场强为E2,方向竖直向上的匀强电场.若质量为m、带电量为+q的小球从上方电场的A点由静止释放,恰好能到达下方电场中与A关于虚线对称的B点,则( )| A. | 场强大小关系满足E2=2E1 | B. | 场强E1不可能大于E2 | ||
| C. | 若AB高度差为h,则UAB=-$\frac{mgh}{q}$ | D. | 带电小球在AB两点电势能相等 |
20. 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
 如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )
如图所示,一长为L的轻质细杆可绕其一端O点在竖直平面内自由转动,在杆的中点和另一端分别固定两个质量相等的可看作质点的A、B小球.重力加速度为g,不计空气阻力.现将杆从水平位置静止释放,下列说法正确的是( )| A. | A球机械能守恒 | |
| B. | A球运动到最低点时,重力的功率为零 | |
| C. | A球到达最低点时的速度为2$\sqrt{\frac{3gL}{5}}$ | |
| D. | 以后A球一定能回到释放点 |
10.某同学将质量为m的一瓶矿泉水竖直向上抛出,水瓶以$\frac{5}{4}$g的加速度匀减速上升,上升的最大高度为H,水瓶往返过程受到的阻力大小不变,则( )
| A. | 上升过程中矿泉水的动能变量为mgH | |
| B. | 上升过程中矿泉水的机械能减少了$\frac{1}{4}$mgH | |
| C. | 水瓶落回地面时动能大小为$\frac{3}{4}$mgH | |
| D. | 水瓶上升过程处于超重状态,下落过程处于失重状态 |
17. 如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )
如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )
 如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )
如图所示,两物体A、B质量相等,相互接触放在光滑水平面上,对物体A施以水平向右推力F1,同时对B施加水平向左推力F2,且F1>F2,则物体B对物体A的作用力大小是( )| A. | $\frac{{F}_{1}-{F}_{2}}{2}$ | B. | $\frac{{F}_{1}+{F}_{2}}{2}$ | C. | $\frac{{F}_{1}}{2}$ | D. | $\frac{{F}_{2}}{2}$ |
14.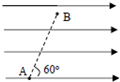 如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )
如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )
 如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )
如图所示,A、B是匀强电场中相距4cm的两点,其连线与电场方向的夹角为60°,两点间的电势差为20V,则电场强度大小为( )| A. | 5V/m | B. | 50V/m | C. | 1×102V/m | D. | 1×103V/m |
 如图所示,在倾角θ=37°的斜面上,N点上方粗糙,下方光滑,一质量为m=0.3kg的物块(可视为质点)从N点上方离N距离为l=2.0m的P点由静止释放,下滑到N处开始压缩弹簧后又被弹离,物块第一次上滑最高位置离N点的距离为l1=1.6m,已知弹簧的劲度系数k=1.6N/m,g=10m/s2,(不计物体与弹簧接触瞬间能量的损失,sin37°=0.6,cos37°=0.8).求:
如图所示,在倾角θ=37°的斜面上,N点上方粗糙,下方光滑,一质量为m=0.3kg的物块(可视为质点)从N点上方离N距离为l=2.0m的P点由静止释放,下滑到N处开始压缩弹簧后又被弹离,物块第一次上滑最高位置离N点的距离为l1=1.6m,已知弹簧的劲度系数k=1.6N/m,g=10m/s2,(不计物体与弹簧接触瞬间能量的损失,sin37°=0.6,cos37°=0.8).求: