题目内容
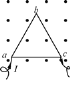
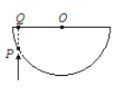
【题目】真空中有一个半球形的玻璃，半径为R，直径所在的圆形截面水平。如图是过球心的竖直半圆形纵截面，在该竖直面内有一束竖直向上的光线从P点射入该玻璃半球。已知入射方向的延长线与圆形截面的交点Q与球心O点的间距为
，该玻璃球的折射率为
，光速为c。求：
①光进入玻璃后，第一次从玻璃射出点到球心O点的距离；
②光在玻璃半球中传播的时间。
【答案】①
；②
【解析】
①入射光线与半球体的交点为P，连接OP，OP为入射点的法线。因此图中的角α为入射角，过P点作球体水平表面的垂线，垂足为Q，设∠QPO=α，
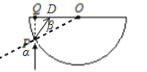
由几何关系有
sin∠QPO=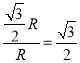
得
α=60°
设光线在C点的折射角为β，有折射定律可得
联立解得
β=30°
由几何关系，∠QOP也是30°，设折射光线与玻璃上表面交于D点，则△OPD为等腰三角形，所以
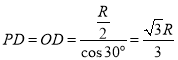
②光在玻璃内的速度
所以光在玻璃半球中传播的时间
联立可得
练习册系列答案
阅读快车系列答案
相关题目
