题目内容
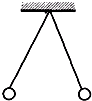
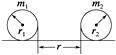
【题目】把质量m=2×10﹣3kg的带负电小球A,用绝缘细绳悬起,若将带电量为QB=4.0×10﹣6C的带电球B靠近A,当两个带电小球在同一高度相距r=0.3m时,绳与竖直方向的夹角为α=45°,如图,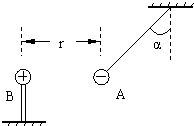
试求:
(1)B球受到的库仑力多大?
(2)A球带电量是多少?
【答案】
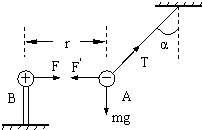
(1)解:依题意,带负电的小球A处于平衡状态,A受到库仑力F'、重力mg以及绳子的拉力T的作用(如图),根据平衡条件,得:mg﹣Tcosα=0
F′﹣Tsinα=0得:F'=mgtanα=2×10﹣3×9.8×1=2×10﹣2(N)根据牛顿第三定律,有:F=F'=2×10﹣2(N)
(2)解:根据库仑定律,得:F'= ![]() 解得:q=
解得:q= ![]() =
= ![]() =5.0×10﹣8(C)
=5.0×10﹣8(C)
【解析】(1)A球受重力、拉力和静电力处于平衡,根据合成法求出A球所受的静电力.(2)根据库仑定律F=k ![]() 求出A球所带的电量.
求出A球所带的电量.
【考点精析】根据题目的已知条件,利用库仑定律的相关知识可以得到问题的答案,需要掌握在真空中两个点电荷间的作用力跟它们的电荷量的乘积成正比,跟它们之间的距离的平方成反比,作用力的方向在它们的连线上;适用条件:真空中的点电荷.

练习册系列答案
相关题目