题目内容
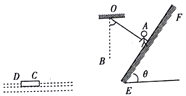
【题目】图为特种兵训练项目的示意图,在水面上的正方形浮台(厚度不计)与斜坡之间悬挂一个不计质量且不可伸长的轻绳绳子的悬点为O,可在竖直平面内摆动。一士兵(视为质点)沿倾角
=53°的斜面滑到A点,此时绳子恰好摆到A处,士兵立即抓住绳子随绳子一起向下摆动(此过程不计机械能的损失),当摆动到最低点B时,士兵松开绳子,然后做平抛运动落到水面浮台正中央。已知OA⊥EF,绳长l=5m,B、C间水平距离s=10m竖直高度h=5m,浮台的边长d=2m,A、B、C、D、E、F在同一竖直平面内,士兵的质量m=60kg,不计空气阻力,取g=10
,sin53°=0.8,cos53°=0.6.求
(1)土兵经过B点时所受绳子的拉力大小;
(2)士兵在斜面上A点的速度大小
【答案】（1）2052N （2）9m/s
【解析】
（1）士兵从B点运动到浮台正中央的过程中做平抛运动。有
由牛顿第二定律得
，联立得
（2）士兵从A 点到B 点的过程机械能守恒，
，解得
练习册系列答案
阅读快车系列答案
相关题目
