题目内容
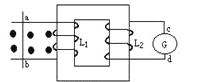
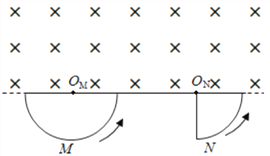
【题目】竖直平行放置的两个金属板A、K连在如图所示电路中，电源电动势E＝91V，内阻r＝1Ω，定值电阻R1＝10Ω，滑动变阻器R2的最大阻值为80Ω，S1、S2为A、K板上的两个小孔，S1与S2的连线水平，在K板的右侧正方形MNPQ区域内有一个水平方向的匀强磁场，磁感应强度大小为B＝0.10T，方向垂直纸面向外。其中正方形MN边与S1S2连线的延长线重合，已知正方形MNPQ的边界有磁场，其边长D＝0.2m，电量与质量之比为
＝2.0×105C/kg的带正电粒子由S1进入电场后，通过S2沿MN射入磁场，粒子从NP边的中点离开磁场，粒子进入电场的初速度、重力均可忽略不计，(sin30°＝0.5，sin37°＝0.6，sin45°＝0.7，π＝3.14)问：
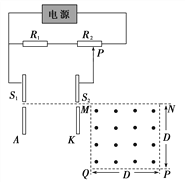
(1)两个金属板A、K各带什么电？(不用说明理由)
(2)粒子在磁场中运动的时间为多长？
(3)滑动变阻器R2的滑片P左端的电阻R2′为多大？(题中涉及数学方面的计算需要写出简要的过程，计算结果保留三位有效数字)
【答案】(1)A板带正电，K板带负电 (2)4.62×10－5s (3)52.5Ω
【解析】 (1)带正电的粒子在电场力作用下向右加速运动，粒子所受电场力水平向右，电场水平向右，则金属板A带正电，金属板K带负电；
(2)粒子在磁场中做匀速圆周运动，
由几何知识得：D2＋(r－
)2＝r2，解得：r＝0.25m，
sinθ＝
＝0.8，则：θ＝53°；
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，
由牛顿第二定律得：qvB＝m
，
粒子做圆周运动的周期： 
，粒子的运动时间：t＝
T，
解得：v＝5×103m/s，t＝4.62×10－5s；
(3)粒子在极板间做加速运动，由动能定理得：qU＝
mv2－0，
由欧姆定律得： 
，
U＝I(R1＋R2′)，解得：R2′＝52.5Ω；
