��Ŀ����
10�� ڤ������̫���Ĺ�ת����Ǹ���Բ����ת����ΪT0������Ϊm������յ�A��̫���ľ���Ϊa��Զ�յ�C��̫���ľ���Ϊb�������ij���Ϊc��A��C��������ʰ뾶��Ϊka��ͨ���õ�������Ͻ��ڸõ������������һԲ���ڼ�������£����Բ�ͽ����õ������Բ����뾶�����õ�����ʰ뾶������ͼ��ʾ����̫��������ΪM��������������ΪG�������������Ƕ�����Ӱ�켰̫���뾶�Ĵ�С��������
ڤ������̫���Ĺ�ת����Ǹ���Բ����ת����ΪT0������Ϊm������յ�A��̫���ľ���Ϊa��Զ�յ�C��̫���ľ���Ϊb�������ij���Ϊc��A��C��������ʰ뾶��Ϊka��ͨ���õ�������Ͻ��ڸõ������������һԲ���ڼ�������£����Բ�ͽ����õ������Բ����뾶�����õ�����ʰ뾶������ͼ��ʾ����̫��������ΪM��������������ΪG�������������Ƕ�����Ӱ�켰̫���뾶�Ĵ�С��������| A�� | ڤ���Ǵ�A��B���õ�ʱ��С��$\frac{{T}_{0}}{4}$ | |
| B�� | ڤ���Ǵ�C��D��A�Ĺ����У����������������Ĺ�Ϊ$\frac{1}{2}$GMmk��$\frac{2}{a}$-$\frac{a}{{b}^{2}}$�� | |
| C�� | ڤ���Ǵ�C��D��A�Ĺ����У����������������Ĺ�Ϊ$\frac{1}{2}$GMmk��$\frac{1}{a}$-$\frac{a}{{b}^{2}}$�� | |
| D�� | ڤ������B��ļ��ٶ�Ϊ$\frac{4GM}{{{{��b-a��}^2}+4{c^2}}}$ |
���� ���������յ������˶������ɣ�
��һ���ɣ����е�����Χ��̫���˶��Ĺ��������Բ��̫������������Բ��һ�������ϣ�
�ڶ����ɣ���ÿһ�����Ƕ��ԣ�̫�����ǵ���������ͬʱ����ɨ���������ȣ�
�������ɣ��������ǵĹ���İ볤������η�����ת���ڵĶ��η��ı�ֵ����ȣ�
���ݹ��ܹ�ϵ֪��������������
��� �⣺A����ת����ΪT0��ڤ���Ǵ�A��C�Ĺ��������õ�ʱ����0.5T0��
����ڤ���Ǵ�A��B��C�Ĺ����У�������С����A��B���B��C��·����ȣ�
����ڤ���Ǵ�A��B���õ�ʱ��С��$\frac{{T}_{0}}{4}$����A��ȷ��
BC�����������������Ĺ��������ܵļ�С�������ڶ��ܵ�������W=$\frac{1}{2}m{v}_{A}^{2}$-$\frac{1}{2}m{v}_{C}^{2}$���������������䵱������֪G$\frac{Mm}{{a}^{2}}$=m$\frac{{v}_{A}^{2}}{ka}$��GM$\frac{m}{{b}^{2}}$=m$\frac{{v}_{C}^{2}}{ka}$������������������������Ĺ�W=$\frac{1}{2}$GMmk��$\frac{1}{a}$-$\frac{a}{{b}^{2}}$������C��ȷ��B����
D����B��̫���ľ���Ϊx����x2=c2$+\frac{��b-a��^{2}}{4}$���������������䵱������֪$\frac{GMm}{{x}^{2}}$=ma��֪ڤ������B��ļ��ٶ�Ϊa=$\frac{4GM}{{{{��b-a��}^2}+4{c^2}}}$����D��ȷ��
��ѡ��ACD
���� ��ȷ������յ������˶��������ǽ����Ĺؼ�������ݹ��ܹ�ϵ�����������䵱���������ܱ仯�������������٣�

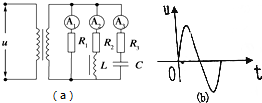 ͼ��a����ʾ��·�У�A1��A2��A3Ϊ��ͬ�ĵ�������CΪ������������R1��R2��R3����ֵ��ͬ����ȦL��ֱ�����費�ƣ��������ѹ��ԭ��Ȧ��������ͼ��b����ʾ��ѹ��������
ͼ��a����ʾ��·�У�A1��A2��A3Ϊ��ͬ�ĵ�������CΪ������������R1��R2��R3����ֵ��ͬ����ȦL��ֱ�����費�ƣ��������ѹ��ԭ��Ȧ��������ͼ��b����ʾ��ѹ��������| A�� | ������A1��A2��ʾ����ͬ | B�� | ������A2��ʾ����A3��С | ||
| C�� | ������A1��ʾ����A2�Ĵ� | D�� | ��������ʾ������ͬ |
| A�� | �ڿ������������������У������Ʋ�����ƫת | |
| B�� | ������Ͷ�����߹�˲�䣬�����Ʒ���ƫת�����������ܹ�ȥ�۲�ʱ���������Ѳ���ƫת | |
| C�� | ���������۲쵽������ƫת��ԭ���ǵ�ʱ�����������Ȳ��� | |
| D�� | ���������۲쵽������ƫת��ԭ���ǵ��߹�����������С |
| A�� | 25N��15N��40N | B�� | 10N��15N��20N | C�� | 10N��20N��40N | D�� | 2N��4N��6N |
| A�� | ���������ľ���С���ӽ���ʱ������֮�������������������� | |
| B�� | ��ֻ��������������ڼ���������֮�䣬����֮�������������ı� | |
| C�� | ���ҵ����������Ĵ�С���ҶԼ����������Ĵ�С����� | |
| D�� | ��m1��m2�����ҵ��������������ҶԼ��������� |
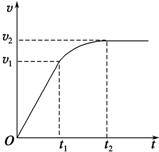 ��ͼ��Ϊ������ˮƽ·�����������̵�v-tͼ��0��t1ʱ����Ϊ�ȼ��ٽΣ�t1��t2ʱ���ڱ�ʾ�Զ������ʻʱ�ı���ٽΣ�t2������t��ƽ�е�ֱ�ߣ��������������������������㶨��������˵����ȷ���ǣ�������
��ͼ��Ϊ������ˮƽ·�����������̵�v-tͼ��0��t1ʱ����Ϊ�ȼ��ٽΣ�t1��t2ʱ���ڱ�ʾ�Զ������ʻʱ�ı���ٽΣ�t2������t��ƽ�е�ֱ�ߣ��������������������������㶨��������˵����ȷ���ǣ�������| A�� | 0��t1ʱ���ڣ�ǣ���������ʲ��� | |
| B�� | 0��t1ʱ���ڣ�ǣ����Ϊ������$\frac{{v}_{2}}{{v}_{1}}$�� | |
| C�� | ��v2=2v1����0��t1ʱ���ڣ�ǣ�������Ĺ�Ϊmv12 | |
| D�� | ��t2=2t1����t1��t2ʱ���ڣ�ǣ�������Ĺ�Ϊmv22��$\frac{{v}_{2}}{{v}_{2}-{v}_{1}}$�� |
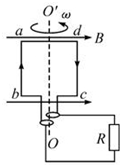 ��ǿ�ų��ĴŸ�Ӧǿ��ΪB���߳�ΪL����������Ȧabcd��N�ѣ���Ȧ����Ϊr����Ȧ�ƴ�ֱ�ڴŸ��ߵ�OO������ͼ��ʾ�Ľ��ٶȦ�����ת�������·����ΪR����
��ǿ�ų��ĴŸ�Ӧǿ��ΪB���߳�ΪL����������Ȧabcd��N�ѣ���Ȧ����Ϊr����Ȧ�ƴ�ֱ�ڴŸ��ߵ�OO������ͼ��ʾ�Ľ��ٶȦ�����ת�������·����ΪR����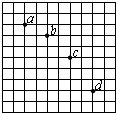 �����о�ƽ���˶���ʵ��ʱ����С������ͬһ����˶���ͨ����㷨����С��ƽ���˶��Ĺ켣������һ��ӡ��С�����ֽ��¼�켣��С����ı߳�Ϊ5cm��С����ƽ���˶�;�еļ���λ����ͼ�е�a��b��c��d��ʾ����С��ƽ�ij��ٶȵĴ�СΪv0=1.4m/s��gȡ9.8m/s2����
�����о�ƽ���˶���ʵ��ʱ����С������ͬһ����˶���ͨ����㷨����С��ƽ���˶��Ĺ켣������һ��ӡ��С�����ֽ��¼�켣��С����ı߳�Ϊ5cm��С����ƽ���˶�;�еļ���λ����ͼ�е�a��b��c��d��ʾ����С��ƽ�ij��ٶȵĴ�СΪv0=1.4m/s��gȡ9.8m/s2����