题目内容
1.利用气垫导轨做实验来验证动量守恒定律:开始时两个滑块静止,它们之间有一根被压缩的轻弹簧,滑块用绳子连接,绳子烧断后,两个滑块向相反方向运动.得到如图所示的两个滑块A、B相互作用后运动过程的频闪照片,频闪的频率为10Hz.已知滑块A、B的质量分别为200g、300g,根据照片记录的信息,A、B离开弹簧后,A滑块做匀速直线运动,其速度大小为0.09 m/s,本次实验中得出的结论是:两滑块组成的系统在相互作用过程中质量和速度乘积的矢量和守恒.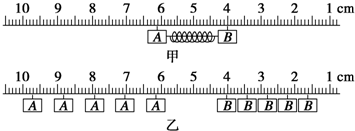
分析 在弹簧弹力作用下的弹性碰撞,动量守恒,据图可知,两物块的运动轨迹均为匀速直线运动,通过刻度读出速度.
解答 解:由题图可知,细绳烧断后,A、B均做匀速直线运动.开始时有:vA=0,vB=0,
A、B被弹开后有:vA′=$\frac{0.009}{\frac{1}{10}}$=0.09m/s,vB′=$\frac{0.006}{\frac{1}{10}}$=0.06m/s,
mAvA′=0.2×0.09=0.018kg•m/s
mBvB′=0.3×0.06=0.018kg•m/s
由此可得:mAvA′=mBvB′,即:0=mBvB′-mAvA′
结论是:两滑块组成的系统在相互作用过程中质量和速度乘积的矢量和守恒.
故答案为:0.09,两滑块组成的系统在相互作用过程中质量和速度乘积的矢量和守恒.
点评 本题考查弹性碰撞问题,明确弹性碰撞中系统的总动量是守恒的;同时注意频率10Hz的意义,并能正确求解对应的时间.

练习册系列答案
相关题目
9.某行星的半径为R,以其第一宇宙速度运行的卫星的周期为T0,又知该行星的一颗同步卫星的线速度的大小为v,不考虑其他星球的影响,仅根据以上物理量不能求出( )
| A. | 该行星的质量M | B. | 该行星的自转周期T | ||
| C. | 该行星表面的重力加速度g | D. | 该同步卫星距离行星表面的高度h |
9.某人用手拉着质量为m的物体由静止向上以加速度a提升h,下列说法中正确的是( )
| A. | 提升过程中物体的动能减小 | B. | 提升过程中合外力对物体做功为零 | ||
| C. | 提升过程中手对物体做功m(a+g)h | D. | 提升过程中物体重力做功mgh |
6. 如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
 如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是( )| A. | 弹簧的弹性势能先增大后减小 | |
| B. | 小球的动能先增大后减小 | |
| C. | 小球的机械能守恒 | |
| D. | 小球与弹簧机械能总和先增大后减小 |
10. 冥王星绕太阳的公转轨道是个椭圆,公转周期为T0,质量为m,其近日点A到太阳的距离为a,远日点C到太阳的距离为b,半短轴的长度为c,A、C两点的曲率半径均为ka(通过该点和曲线上紧邻该点两侧的两点作一圆,在极限情况下,这个圆就叫做该点的曲率圆,其半径叫做该点的曲率半径),如图所示.若太阳的质量为M,万有引力常量为G,忽略其他行星对它的影响及太阳半径的大小,则( )
冥王星绕太阳的公转轨道是个椭圆,公转周期为T0,质量为m,其近日点A到太阳的距离为a,远日点C到太阳的距离为b,半短轴的长度为c,A、C两点的曲率半径均为ka(通过该点和曲线上紧邻该点两侧的两点作一圆,在极限情况下,这个圆就叫做该点的曲率圆,其半径叫做该点的曲率半径),如图所示.若太阳的质量为M,万有引力常量为G,忽略其他行星对它的影响及太阳半径的大小,则( )
 冥王星绕太阳的公转轨道是个椭圆,公转周期为T0,质量为m,其近日点A到太阳的距离为a,远日点C到太阳的距离为b,半短轴的长度为c,A、C两点的曲率半径均为ka(通过该点和曲线上紧邻该点两侧的两点作一圆,在极限情况下,这个圆就叫做该点的曲率圆,其半径叫做该点的曲率半径),如图所示.若太阳的质量为M,万有引力常量为G,忽略其他行星对它的影响及太阳半径的大小,则( )
冥王星绕太阳的公转轨道是个椭圆,公转周期为T0,质量为m,其近日点A到太阳的距离为a,远日点C到太阳的距离为b,半短轴的长度为c,A、C两点的曲率半径均为ka(通过该点和曲线上紧邻该点两侧的两点作一圆,在极限情况下,这个圆就叫做该点的曲率圆,其半径叫做该点的曲率半径),如图所示.若太阳的质量为M,万有引力常量为G,忽略其他行星对它的影响及太阳半径的大小,则( )| A. | 冥王星从A→B所用的时间小于$\frac{{T}_{0}}{4}$ | |
| B. | 冥王星从C→D→A的过程中,万有引力对它做的功为$\frac{1}{2}$GMmk($\frac{2}{a}$-$\frac{a}{{b}^{2}}$) | |
| C. | 冥王星从C→D→A的过程中,万有引力对它做的功为$\frac{1}{2}$GMmk($\frac{1}{a}$-$\frac{a}{{b}^{2}}$) | |
| D. | 冥王星在B点的加速度为$\frac{4GM}{{{{(b-a)}^2}+4{c^2}}}$ |
 某物理学习小组用如图所示装置做“探究功与速度变化的关系”实验
某物理学习小组用如图所示装置做“探究功与速度变化的关系”实验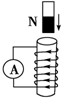
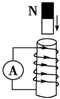
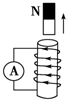
 如图所示,水平面上有同种材料制成的质量相等的A、B、C三个小滑块,轻弹簧的一端固定,另一端与滑块C相连,C静止在水平面上的O点,此时弹簧处于原长.已知OP=L,B位于OP中点.滑块A从P点以初速度v0向B滑行并与B相碰,碰后A、B黏在一起又继续滑行与C相碰,碰后A、B与C黏在一起.设滑块碰撞时间极短,滑块A、B、C均可视为质点,滑块与水平面间的动摩擦因数均为μ,重力加速度为g.
如图所示,水平面上有同种材料制成的质量相等的A、B、C三个小滑块,轻弹簧的一端固定,另一端与滑块C相连,C静止在水平面上的O点,此时弹簧处于原长.已知OP=L,B位于OP中点.滑块A从P点以初速度v0向B滑行并与B相碰,碰后A、B黏在一起又继续滑行与C相碰,碰后A、B与C黏在一起.设滑块碰撞时间极短,滑块A、B、C均可视为质点,滑块与水平面间的动摩擦因数均为μ,重力加速度为g. 某同学做了“测定玩具枪子弹与透明物块相互作用力”的实验,如图所示,将质量为m的子弹以速度v0沿水平方向射入固定在光滑水平面上质量为M的透明物块中,测得子弹射入的深度为d,设子弹与物块之间的相互作用力的大小与物块的运动状态无关.请你帮该同学计算:
某同学做了“测定玩具枪子弹与透明物块相互作用力”的实验,如图所示,将质量为m的子弹以速度v0沿水平方向射入固定在光滑水平面上质量为M的透明物块中,测得子弹射入的深度为d,设子弹与物块之间的相互作用力的大小与物块的运动状态无关.请你帮该同学计算: