题目内容
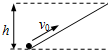 如图(a)所示,小球的初速度为v0,沿光滑斜面上滑,能上滑的最大高度为h,在图(b)中,四个物体的初速度均为v0.在A图中,小球沿一光滑内轨向上运动,内轨半径大于h;在B图中,小球沿一光滑内轨向上运动,内轨半径小于h;在图C中,小球沿一光滑内轨向上运动,内轨直径等于h;在D图中,小球固定在棒的下端,棒的长度为h的一半,小球随棒绕O点向上转动.则小球上升的高度能达到h的有( )
如图(a)所示,小球的初速度为v0,沿光滑斜面上滑,能上滑的最大高度为h,在图(b)中,四个物体的初速度均为v0.在A图中,小球沿一光滑内轨向上运动,内轨半径大于h;在B图中,小球沿一光滑内轨向上运动,内轨半径小于h;在图C中,小球沿一光滑内轨向上运动,内轨直径等于h;在D图中,小球固定在棒的下端,棒的长度为h的一半,小球随棒绕O点向上转动.则小球上升的高度能达到h的有( )A、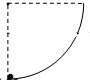 | B、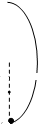 | C、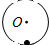 | D、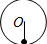 |
分析:小球沿光滑斜面上滑,能上滑的最大高度为h,知道小球到达最高点时的速度为零.通过判断选项中各图最高点的速度能否为零来判断上升的高度能否到达h.
解答:解:由题意,a图中,由机械能守恒得:mgh=
m
,得:h=
A、小球沿一光滑内轨向上运动,内轨半径大于h,设小球上升的最大高度为H时速度为零,根据机械能守恒定律得:
m
=mgH
得:H=
=h.故A正确.
B、小球沿一光滑内轨向上运动,内轨半径小于h,小球离开轨道后做斜上抛运动,上升到最大高度时,速度v>0,根据机械能守恒得:
m
=mgH+
mv2,得:H<
=h.故B错误.
C、小球沿一光滑内轨向上运动,内轨直径等于h,在最高点有最小速度,则知小球未到达最高点已离开轨道.故C错误.
D、小球固定在轻杆的下端,轻杆的长度为h的一半,小球随轻杆绕O点向上转动.最高点的最小速度为零,小球能够达到最高点.故D正确.
故选:AD.
| 1 |
| 2 |
| v | 2 0 |
| ||
| 2g |
A、小球沿一光滑内轨向上运动,内轨半径大于h,设小球上升的最大高度为H时速度为零,根据机械能守恒定律得:
| 1 |
| 2 |
| v | 2 0 |
得:H=
| ||
| 2g |
B、小球沿一光滑内轨向上运动,内轨半径小于h,小球离开轨道后做斜上抛运动,上升到最大高度时,速度v>0,根据机械能守恒得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| ||
| 2g |
C、小球沿一光滑内轨向上运动,内轨直径等于h,在最高点有最小速度,则知小球未到达最高点已离开轨道.故C错误.
D、小球固定在轻杆的下端,轻杆的长度为h的一半,小球随轻杆绕O点向上转动.最高点的最小速度为零,小球能够达到最高点.故D正确.
故选:AD.
点评:本题主要运动的规律时机械能守恒定律,关键是判断在h高度速度是否为零,从而判断是否能到达h高度.

练习册系列答案
相关题目
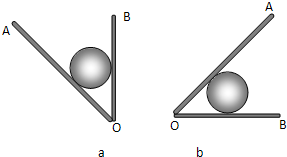 如图(a)所示,小球放置在光滑V形槽中,初始槽板OB处竖直平面,将V形槽沿顺时针绕槽底角O点缓慢转动90°,到OB处水平平面,如图(b)所示.在这个过程中,板OB受到的压力将
如图(a)所示,小球放置在光滑V形槽中,初始槽板OB处竖直平面,将V形槽沿顺时针绕槽底角O点缓慢转动90°,到OB处水平平面,如图(b)所示.在这个过程中,板OB受到的压力将 (1)(单选题)用细线将一块玻璃片水平地悬挂在弹簧测力计的下端,并使玻璃片贴在水面上,如图所示,然后用手缓慢提起弹簧测力计,在使玻璓片脱离水面的一瞬间,关于弹簧测力计的示数下列说法中正确的是
(1)(单选题)用细线将一块玻璃片水平地悬挂在弹簧测力计的下端,并使玻璃片贴在水面上,如图所示,然后用手缓慢提起弹簧测力计,在使玻璓片脱离水面的一瞬间,关于弹簧测力计的示数下列说法中正确的是