��Ŀ����
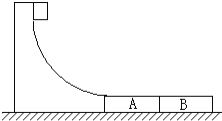
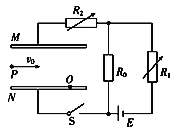
����Ŀ����ͼ����ʾ����ˮƽ���õ����浼������һ���з��еĻ��飬����ΪM�����浼���Ҷ˹̶�һ�����֣�ϸ���ƹ����֣�һ���뻬����������һ�˹���6�����룬��ÿ�����������Ϊm����M=4m��

��1�����α꿨�߲�������ϵĵ���Ƭ�Ŀ��ȣ�������ͼ����ʾ�������d=_________cm����2��ijͬѧ����Դ���������ɾ�ֹ�ͷţ������ϵĵ���Ƭͨ������ŵ�ʱ��Ϊt����ͨ������ŵ��ٶ�Ϊ___��������������ĸ��ʾ����
��3����ʼʵ��ʱ��ϸ����һ�˹���6�����룬�ɾ�ֹ�ͷź�ϸ���ϵ�����ΪF1������ÿ��ʵ��ʱ��1�������Ʒŵ������ϵķ����У���ֻʣ3������ʱϸ���ϵ�����ΪF2����F1___2F2��������������������������С��������
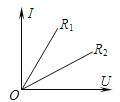
��4����ÿ���ƶ������ͬһλ���ͷŻ��飬�赲��Ƭ�����ŵľ���ΪL������ĸ���Ϊn�����ÿ�ε���Ƭͨ������ŵ�ʱ��Ϊt������������ݣ������n-1/t2ͼ����֪ͼ��б��Ϊk�����������ٶ�Ϊ___����������ĸ��ʾ����
���𰸡� 0.520cm ![]() С��
�� ![]()
��������(1)�α꿨�ߵ����߶���Ϊ5mm���α����Ϊ0.05��4mm=0.20mm�������ն���Ϊ5.20mm=0.520cm.
(2)����ʱ���ڵ�ƽ���ٶȵ���˲ʱ�ٶȵĴ�С,��ͨ������ŵ��ٶ�![]()
(3)���������![]() ������Ի������,����ţ�ٵڶ����ɵ�,F1=Ma1=4m��0.6g=2.4mg��
������Ի������,����ţ�ٵڶ����ɵ�,F1=Ma1=4m��0.6g=2.4mg��
![]() ������Ի������,����ţ�ٵڶ����ɵ�,F2=7ma2=2.1mg,֪F1<2F2.
������Ի������,����ţ�ٵڶ����ɵ�,F2=7ma2=2.1mg,֪F1<2F2.
(4)����ͨ������ŵ��ٶ�![]() ��
��
����v2=2aL�� ![]() ��
��
��Ϊ![]() ,������
,������![]() ��
��
ͼ�ߵ�б��![]() �����
�����![]()

 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д�