题目内容
14.质量为0.3kg的小球在水平面上做匀速圆周运动.小球的转动半径为0.2m,每0.1s转过π(弧度).求:(要求计算结果保留π)(1)求角速度、线速度、周期;
(2)求向心加速度和向心力.
分析 (1)根据角速度的定义式求出角速度的大小,结合角速度与线速度的关系v=rω求出线速度的大小,根据T=$\frac{2π}{ω}$求出周期的大小.
(2)根据向心加速度公式a=rω2求出向心加速度的大小,根据F=ma求出向心力.
解答 解:(1)角速度$ω=\frac{△θ}{△t}=\frac{π}{0.1}rad/s=10πrad/s$.
线速度v=rω=0.2×10πm/s=2πm/s.
周期T=$\frac{2π}{ω}=\frac{2π}{10π}s=0.2s$.
(2)向心加速度a=rω2=0.2×100π2=20π2m/s2,
向心力F=ma=0.3×20π2=6π2N.
答:(1)角速度为10πrad/s,线速度为2πm/s,周期为0.2s.
(2)向心加速度为20π2m/s2,向心力为6π2N.
点评 本题考查了角速度、线速度、周期、向心力、向心加速度的基本运用,掌握这些物理量之间的联系,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.一个质量为m的硬币放在一转盘上,距离轴心r,转盘由静止开始转动,角加速度为α,若硬币保持随转盘一起转动且无滑动,若t秒后硬币恰好开始滑动,则硬币与转盘间的静摩擦系数为( )
| A. | $\frac{rα\sqrt{1+{α}^{2}{t}^{4}}}{g}$ | B. | $\frac{rα\sqrt{1-{α}^{2}{t}^{4}}}{g}$ | C. | $\frac{{r}^{2}α}{g}$ | D. | $\frac{r{α}^{2}{t}^{2}}{g}$ | ||||
| E. | $\frac{rα}{g}$ |
19.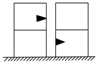 矩形滑块由不同材料的上下两层粘结在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射入滑块,若射击上层,则子弹刚好不穿出;若射击下层,整个子弹刚好嵌入,则上述两种情况相比较( )
矩形滑块由不同材料的上下两层粘结在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射入滑块,若射击上层,则子弹刚好不穿出;若射击下层,整个子弹刚好嵌入,则上述两种情况相比较( )
 矩形滑块由不同材料的上下两层粘结在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射入滑块,若射击上层,则子弹刚好不穿出;若射击下层,整个子弹刚好嵌入,则上述两种情况相比较( )
矩形滑块由不同材料的上下两层粘结在一起组成,将其放在光滑的水平面上,如图所示,质量为m的子弹以速度v水平射入滑块,若射击上层,则子弹刚好不穿出;若射击下层,整个子弹刚好嵌入,则上述两种情况相比较( )| A. | 两次子弹对滑块做的功一样多 | |
| B. | 两次滑块受的冲量一样大 | |
| C. | 子弹嵌入下层过程中克服阻力做功较少 | |
| D. | 子弹射入上层过程中系统产生的热量较多 |
8.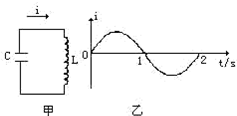 如图甲所示的LC回路中,电流的变化规律如图乙所示,把顺时针的方向规定为电流正方向,则( )
如图甲所示的LC回路中,电流的变化规律如图乙所示,把顺时针的方向规定为电流正方向,则( )
 如图甲所示的LC回路中,电流的变化规律如图乙所示,把顺时针的方向规定为电流正方向,则( )
如图甲所示的LC回路中,电流的变化规律如图乙所示,把顺时针的方向规定为电流正方向,则( )| A. | 0.5s至1.0s时间内,电容器在充电 | |
| B. | 0.5s至1.0s时间内,电容器上极板带正电荷 | |
| C. | 1.0s至1.5s时间内,电感线圈中的自感电动势在减小 | |
| D. | 0.5s至1.5s时间内,磁场能和电场能完成了一次周期性的变化 |
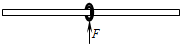 如图所示,一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上,环的半径略大于杆的半径.环与杆之间的动摩擦因数为μ,t=0时刻给环一个向右的初速度v0,同时对环施加一个方向始终竖直向上的力F,已知力F的大小F=kv(k为常数,v为环的运动速度),且有kv0>mg.t=t1时刻环开始沿杆做匀速直线运动,试求:
如图所示,一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上,环的半径略大于杆的半径.环与杆之间的动摩擦因数为μ,t=0时刻给环一个向右的初速度v0,同时对环施加一个方向始终竖直向上的力F,已知力F的大小F=kv(k为常数,v为环的运动速度),且有kv0>mg.t=t1时刻环开始沿杆做匀速直线运动,试求:
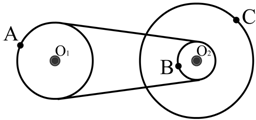 如图所示的皮带传动装置,主动轮O1为2r,从动轮O2上的大小两轮固定在同一个轴心O2上,半径分别为3r和r,A、B、C分别为轮缘上的点,设皮带不打滑,则A、B、C三点的线速度大小之比为1:1:3,角速度之比为1:2:2.
如图所示的皮带传动装置,主动轮O1为2r,从动轮O2上的大小两轮固定在同一个轴心O2上,半径分别为3r和r,A、B、C分别为轮缘上的点,设皮带不打滑,则A、B、C三点的线速度大小之比为1:1:3,角速度之比为1:2:2.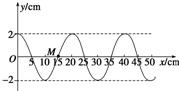 简谐波沿x轴传播,波源的振动周期T=2s.t=0时的波形如图所示,M处的质点此时正经过平衡位置沿y轴正方向运动.画出t=1.5s时的波形图.
简谐波沿x轴传播,波源的振动周期T=2s.t=0时的波形如图所示,M处的质点此时正经过平衡位置沿y轴正方向运动.画出t=1.5s时的波形图.