题目内容
如图所示,一个上表面光滑的斜面体M置于水平地面上,它的两个斜面与水平面间的夹角分别为α、β,且α<β,M的顶端装有一定滑轮,一轻质细绳跨过定滑轮后连接A、B两个小物块,细绳与各自的斜面平行,不计绳与滑轮间的摩擦,A、B恰好在同一高度处于静止状态,剪断细绳后,A、B滑至斜面底端,M始终保持静止,则( )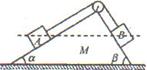
A.物块A的质量大于B的质量
B.物块A对斜面体M的压力大于B对斜面体M的压力
C.两物块达到斜面底端时,物块A重力的瞬时功率较大
D.在滑块A、B下滑的过程中,斜面体受到水平向左的摩擦力
ABD
解析试题分析:对物块均受重力mg、斜面的支持力N和绳的拉力T作用,起初装置处于静止状态,因此根据共点力平衡条件有:T=mAgsinα=mBgsinβ,NA=Tcotα,NB=Tcotβ,由于α<β,所以,mA>mB,NA>NB,故选项A正确;又由牛顿第三定律可知,物块对斜面的压力与斜面对物块的支持力大小相等,故选项B正确;设物块开始离地面的高度为h,根据动能定理可知,物块滑至斜面底端时的速度大小为:v= ,即两物块滑至斜面底端时速度大小相等,根据功率的计算式可知,两物块达到斜面底端时重力的瞬时功率为:PA=mAgvsinα,PB=mBgvsinβ,所以有:PA=PB,故选项C错误;在滑块A、B下滑的过程中,分别对两物块,根据牛顿第二定律有:mAgsinα=mAaA,mBgsinβ=mBaB,对整体受重力(M+mA+mB)g、地面的支持力F和摩擦力f作用,并设摩擦力f的方向水平向右,建立水平和竖直方向的直角坐标系,根据牛顿第二定律,在水平方向上有:f=mBaBcosβ-mAaAcosα=mBgsinβcosβ-mAgsinαcosα,由于α<β,所以,cosβ<cosα,即f<0,说明其方向与假设的方向相反,即水平向左,故选项D正确。
,即两物块滑至斜面底端时速度大小相等,根据功率的计算式可知,两物块达到斜面底端时重力的瞬时功率为:PA=mAgvsinα,PB=mBgvsinβ,所以有:PA=PB,故选项C错误;在滑块A、B下滑的过程中,分别对两物块,根据牛顿第二定律有:mAgsinα=mAaA,mBgsinβ=mBaB,对整体受重力(M+mA+mB)g、地面的支持力F和摩擦力f作用,并设摩擦力f的方向水平向右,建立水平和竖直方向的直角坐标系,根据牛顿第二定律,在水平方向上有:f=mBaBcosβ-mAaAcosα=mBgsinβcosβ-mAgsinαcosα,由于α<β,所以,cosβ<cosα,即f<0,说明其方向与假设的方向相反,即水平向左,故选项D正确。
考点:本题综合考查了瞬时功率的计算、共点力平衡条件、动能定理(或机械能守恒定律)、牛顿运动定律的应用以及假设法、控制变量法、整体法与隔离法的灵活运用问题,属于中档偏高题。

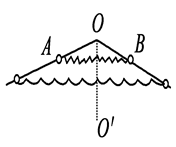
如图所示,a,b,C三根绳子完全相同,其中b绳水平,C绳下挂一重物。若使重物加重,则这三根绳子中最先断的是 ( )
| A.a绳 | B.b绳 | C.C绳 | D.无法确定 |
下列说法正确的是( )
| A.竖直上抛物体到达最高点时,物体处于平衡状态 |
| B.电梯匀速上升时,电梯中的人不处于平衡状态 |
| C.在小车的水平光滑表面上静置一小木块,当平板车加速运动时,小物块仍处于平衡状态 |
| D.竖直弹簧上端固定,下端挂一重物,平衡后,用力F将它再拉下一段距离后停止,当突然撤去力F时,重物仍处于平衡状态 |
如图所示,质量均可忽略的轻绳与轻杆承受弹力的最大值一定, 轻杆A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计), 轻杆B端吊一重物G,现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉(均未断),在AB杆达到竖直前,以下分析正确的是( )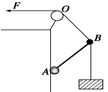
| A.绳子越来越容易断 |
| B.绳子越来越不容易断 |
| C.AB杆越来越容易断 |
| D.AB杆越来越不容易断 |
倾角为α、质量为M的斜面体静止在水平桌面上,质量为m的木块静止在斜面体上。下列结论正确的是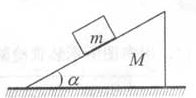
| A.木块受到的摩擦力大小是mgcosα |
| B.木块对斜面体的压力大小是mg sinα |
| C.桌面对斜面体的摩擦力大小是mg sinαcosα |
| D.桌面对斜面体的支持力大小是(M+m)g |
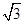 N,则下列说法中错误的是( ) (取g=10 m/s2)
N,则下列说法中错误的是( ) (取g=10 m/s2)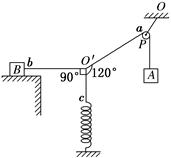
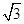 h,劲度系数为k,现在把两个小环在竖直方向上均向下平移h,释放瞬间A环加速度为a,则下列表达式正确的是( )
h,劲度系数为k,现在把两个小环在竖直方向上均向下平移h,释放瞬间A环加速度为a,则下列表达式正确的是( )