��Ŀ����
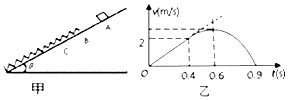
����Ŀ����ͼ���⻬ˮƽֱ�����������������Ϊm�����A��B��C�� ���B��C��ֹ��B�����̶�һ�ᵯ�ɣ��������ĵ����������ƣ�����A���ٶ�v0��B�˶���ѹ�����ɣ���A��B�ٶ����ʱ��B��Cǡ��������ճ����һ��Ȼ������˶�������B��C��ײ����ʱ�伫�̣����A��ʼѹ������ֱ���뵯�ɷ���Ĺ����У�![]()
��1��A��B��һ���ٶ���ͬʱ���ٶȴ�С��
��2��A��B�ڶ����ٶ���ͬʱ���ٶȴ�С��
��3�����������е�����������Ƕ��٣�
���𰸡�
��1���⣺��A��B�Ӵ��Ĺ����У�����һ���ٶ���ͬʱ��ȡ����Ϊ�������ɶ����غ㶨�ɵã�
mv0=2mv1
��ã�v1= ![]() v0
v0
�� A��B��һ���ٶ���ͬʱ���ٶȴ�СΪ ![]() v0��
v0��
��2���⣺��A��B�ڶ����ٶ���ͬʱ���ٶȴ�Сv2����ABCϵͳ��ȡ����Ϊ�������ݶ����غ㶨�ɵã�
mv0=3mv2
��ã�v2= ![]() v0��
v0��
��A��B�ڶ����ٶ���ͬʱ���ٶȴ�СΪ ![]() v0��
v0��
��3���⣺B��C�Ӵ���˲�䣬B��C��ɵ�ϵͳ�����غ㣬������Ϊ�������ɶ����غ㶨�ɵã�
m ![]() v0=2mv3��
v0=2mv3��
���BCճ�Ӻ�˲�乲ͬ�ٶ�Ϊ��v3= ![]() v0��
v0��
��A��B��C�ٶ���ͬʱ�����ɵĵ����������ʱ�У�v2= ![]() v0��
v0��
���������غ㶨�ɵã����ɵ����������Ϊ��Epm= ![]() mv02����
mv02���� ![]() mv12��
mv12�� ![]() 2mv32����
2mv32���� ![]() 3mv22��
3mv22��
������ã�Epm= ![]() mv02��
mv02��
�𣺵��������е������������= ![]() mv02��
mv02��
����������1���ӿ�ʼ��ײ����һ���ٶ��������ϵͳ�����غ���ݶ����غ���ʽ��⡣
��2���ӵ�һ���ٶ���ȵ��ڶ����ٶ����ͬ�����㶯���غ���ݶ����غ���ʽ��⡣
��3����B��C�Ӵ���ϵͳ����ϵͳ���ٵĶ���ȫ��ת��Ϊ���ɵĵ������ܡ�
�����㾫����������Ĺؼ���������ܹ�ϵ�����֪ʶ�����յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1���Լ��Զ����غ㶨�ɵ����⣬�˽���غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�