题目内容
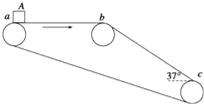
【题目】如图所示,传送带的水平部分ab=2m,斜面部分bc=4m,bc与水平面的夹角α=37°.一个小物体A与传送带的动摩擦因数μ=0.25,传送带沿图示的方向运动,速率v=2m/s.若把物体A轻放到a处,它将被传送带送到c点,且物体A不会脱离传送带.求物体A从a点被传送到c点所用的时间.(已知:sin 37°=0.6,cos 37°=0.8,g=10m/s2)
【答案】2.4 s
【解析】试题分析:物体在水平传送带上先做匀加速直线运动,达到传送带速度后做匀速直线运动,在倾斜传送带上,由于重力沿斜面方向的分力大于滑动摩擦力,所以物体做匀加速直线运动,根据牛顿第二定律求出在水平传送带和倾斜传送带上的加速度,结合运动学公式进行求解.
解:物体A轻放在a点后在摩擦力作用下向右做匀加速直线运动直到和传送带速度相等.在这一过程中有a1=![]() =μg
=μg
x1=![]() ="0.8" m<ab.
="0.8" m<ab.
经历时间为t1=![]() =
=![]() ="0.8" s.
="0.8" s.
此后随传送带运动到b点的时间为t2=![]() ="0.6" s.
="0.6" s.
当物体A到达bc斜面时,由于mgsin 37°=0.6mg>μmgcos 37°=0.2mg.所以物体A将再次沿传送带做匀加速直线运动,
其加速度大小为a2="gsin" 37°﹣μgcos 37°="4" m/s2,
物体A在传送带bc上所用时间满足xbc=vt3+![]() a2t
a2t![]() ,代入数据得t3="1" s.(负值舍去)
,代入数据得t3="1" s.(负值舍去)
则物体A从a点被传送到c所用时间为t=t1+t2+t3="2.4" s.
答:物体A从a点被传送到c点所用的时间为2.4s.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目