题目内容
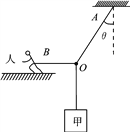
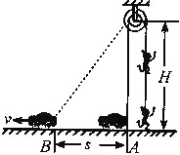
【题目】影视中的武林高手展示轻功时都是吊威亚(钢丝)的,当轨道车通过绳索拉动轴承转动,轮上的钢丝就带动演员上升,便可呈现出飞檐走壁的效果。如图所示,若特技演员的质量m=50kg(人和车可视为质点),g取10m/s2,导演在某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1。若轨道车从图中A沿直线以v=5m/s的速度匀速前进s=6m到B处,则以下说法中不正确的有( )
A. 演员也是匀速上升的
B. 车在B点时,演员具有竖直向上的速度3m/s
C. 在此过程中钢丝对演员的拉力大于重力
D. 在此过程中钢丝对演员做的功为2900J
【答案】AB
【解析】
将车的速度v分解可知拉绳的速度为vcosθ,则随着车从A向B运动,则θ减小,拉绳的速度逐渐变大,则演员的速度也是逐渐变大,即向上加速上升,根据牛顿第二定律可知在此过程中钢丝对演员的拉力大于重力,选项A错误,C正确;设轨道车在B时细线与水平方向之间的夹角为θ,将此时车的速度分解,此时绳索的速度![]() ,由于轮和轴的角速度相同,则其线速度之比等于半径(直径)之比为2:1,v人=2v绳=6m/s。故B错误。根据动能定理得:合力做功W合=△Ek=
,由于轮和轴的角速度相同,则其线速度之比等于半径(直径)之比为2:1,v人=2v绳=6m/s。故B错误。根据动能定理得:合力做功W合=△Ek=![]() mv人2=900J,合力做功W合=△Ek=WG+W拉。W拉=mgh+△Ek=2900J。故D正确;此题选择不正确的选项,故选AB。
mv人2=900J,合力做功W合=△Ek=WG+W拉。W拉=mgh+△Ek=2900J。故D正确;此题选择不正确的选项,故选AB。

练习册系列答案
相关题目