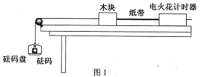
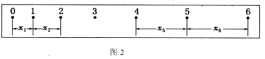
题目内容
【题目】有一倾角θ=30°的斜面与一半径为R的半圆弧轨道AB相切于B点,均固定置于竖直平面内,其中B点为圆弧的最低点。现从斜面上C点无初速释放一质量为m的小球,它沿斜面下滑从B点进入圆轨道内侧。小球进入圆轨道时无能量损失,不计一切摩擦,已知重力加速度g=10m/s2。
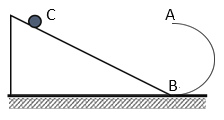
(1)若小球恰好能通过最高点A,则小球出发点C与B点间距离X满足什么要求?
(2)分析小球在圆弧轨道内能到达的最大高度H与小球出发点A和B点间距离X之间的关系。
【答案】(1)5R(2)H=R+Rsinθ=(R+x)/3 (2R<R<5R);
【解析】
(1)设小球在A点速度大小为vA,小球到达A点由重力提供向心力得:
![]()
可得:![]()
研究小球从C到A由机械能守恒定律可得: mgxsinθ=![]() mvA2+mg2R
mvA2+mg2R
解得 x=5R
(2)分三种情况讨论:a.能到最高点,H=2R (X≧5R)
b.只能到与圆心等高点,H=![]() X (X≦2R)
X (X≦2R)
c.能过圆心等高点但到不了最高点:
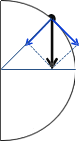
根据机械能守恒定律可列:mgxsin30°=mg(R+Rsinθ)+![]() mv2
mv2
根据牛顿第二定律:![]()
解得:H=R+Rsinθ=(R+x)/3 (2R<R<5R)

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目