题目内容
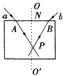
【题目】如图，光滑斜面的倾角
，在斜面上放置一矩形线框 abcd ， ab 边的边长 l 1 =1m， bc 边的边长
，线框的质量 m =1kg，电阻 R = 0.1Ω，线框通过细线与重物相连，重物质量
，斜面上 ef 线（ ef ∥ gh ）的右方有垂直斜面向上的匀强磁场，磁感应强度
，如果线框从静止开始运动，进入磁场最初一段时间是匀速的， ef 线和 gh 的距离
，（取g = 10.4m/s 2 ），求：
（1）线框进入磁场前重物 M 的加速度；
（2）线框进入磁场时匀速运动的速度 v ；
【答案】（1）
（2）6m/s
【解析】本题考查电磁感应中的线框问题，涉及牛顿运动定律应用中的连接体模型。
（1）线框进入磁场前，线框受到线框重力、细线的拉力 F T 、斜面的支持力，重物 M 受到重力和拉力 F T 。
对线框由牛顿第二定律得
对重物
联立解得线框进入磁场前重物 M 的加速度
（2）因为线框进入磁场的最初一段时间做匀速运动，所以重物受力平衡
线框受力平衡
ab 边进入磁场切割磁感线，产生的电动势
线框中的电流
联立上述各式得
，代入数据解得
【题目】某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为97.50 cm，摆球直径为2.00 cm，然后用秒表记录了单摆振动50次所用的时间，如图所示，则：
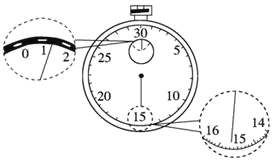
(1)该摆摆长为______cm，秒表所示读数为______s.
(2)如果测得的g值偏小，可能的原因是( )
A．测摆线长时摆线拉得过紧 |
B．摆线上端悬点未固定，振动中出现松动，使摆线长度增加了 |
C．开始计时时，秒表过迟按下 |
D．实验中误将49次全振动记为50次 |
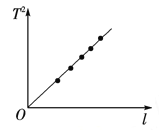
(3)为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据，再以l为横坐标，T2为纵坐标，将所得数据连成直线如图所示，并求得该直线的斜率为k，则重力加速度g＝______(用k表示)．
