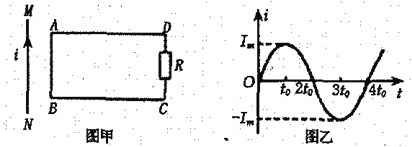
题目内容
【题目】低空跳伞大赛受到各国运动员的喜爱。如图所示为某次跳伞大赛运动员在一座高为H=179m的悬崖边跳伞时的情景。运动员离开悬崖时先做自由落体运动，一段时间后，展开降落伞，以a=8m/s2的加速度匀减速下降，已知运动员和伞包的总质量为80kg，为了运动员的安全，运动员落地时的速度不能超过4m/s，求：
(1) 运动员(含伞包)展开降落伞后所受的空气阻力f；
(2) 为了运动员的安全，展开伞时的最大速度是多少?
(3) 如果以下落的快慢决定比赛的胜负，为了赢得比赛的胜利，运动员在空中运动的最短时间是多大?
【答案】（1）1440N，竖直向上；（2）40 m/s；（3）8.5 s
【解析】试题分析：(1) 根据牛顿第二定律可解得运动员所受的阻力；
(2)利用运动员整个过程所下落的高度等运动员自由下落和匀减速的位移之和，即可求解出运动员展开伞时的速度；
(3)分别求出运动员自由下落的时间和匀减速的时间即为运动员在空中运动的时间。
解：(1)根据牛顿第二定律可知， 
，即
；
(2)从运动员展开伞到落地过程，设运动员展开伞时速度为
，由运动学知识可得： 
，其中
， 
， 
，代入数据解得： 
；
(3)设运动员在空中的最短时间为t，则有：自由下落时间为： 
，运动员展开伞到落地过程的时间为： 
，所以时间
。
点晴：解决本题关键是分析清楚运动员整个过程的运动情形，开始运动员做自由落体，展开伞后做匀减速运动，根据牛顿第二定律和匀变速运动的规律即可求解。
练习册系列答案
全能测控期末小状元系列答案
相关题目
