题目内容
A、B两个小球由柔软的细线相连,线长l=6 m;将A、B球先后以相同的初速度v0=4.5 m/s,从同一点水平抛出(先A后B),相隔时间Δt=0.8 s.
(1)A球抛出后经多少时间,细线刚好被拉直?
(2)细线刚被拉直时,A、B球的水平位移(相对于抛出点)各多大?(g取10 m/s2)
【答案】
(1)1 s (2)A球的水平位移为4.5 m,B球的水平位移为0.9 m
【解析】 (1)两球水平方向位移之差恒为Δx= v0×Δt=4.5×0.8 m=3.6 m,(2分)
AB竖直方向的位移差随时间变化,当竖直方向位移差与水平方向位移差的合位移差等于6 m时绳被拉直.
由水平方向位移差3.6 m,绳子长6 m,可以求得竖直方向位移差为h时绳绷紧.
h=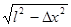 = m=4.8 m(2分),
= m=4.8 m(2分),
有 h=gt2-g(t-0.8 s)2=4.8 m(2分),得t=1 s(2分).
(2)细线刚被拉直时,A球的水平位移为4.5×1 m=4.5 m(2分),
B球的水平位移为4.5×(1-0.8) m=0.9 m.(2分)

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目