题目内容
20.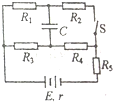 如图所示,电源电动势E=12V,内阻r=1.0Ω,电阻R1=R2=6.0Ω,R3=3.0Ω,R4=9.0Ω,R5=5.0Ω,电容C=4.0×102μF.电键S闭合.
如图所示,电源电动势E=12V,内阻r=1.0Ω,电阻R1=R2=6.0Ω,R3=3.0Ω,R4=9.0Ω,R5=5.0Ω,电容C=4.0×102μF.电键S闭合.(1)求电容器所带电荷量.
(2)将电键S断开,求S断开后通过电阻R1的电荷量.
分析 (1)闭合电键后,根据闭合电路欧姆定律比较出电容器上下两端点的电势高低,从而得出两端的电势差,确定电容器两极板的带电;
(2)电键S断开时,电容器的电压即为R3的电压,电容器的上级板与电源正极相连,确定下极板带负电,求出R3的电压,根据Q=CU求出电荷量的大小,从而得出通过电流计R1的电荷量.
解答 解:(1)电键S闭合时,R1与R2串联,R上=R1+R2=6+6=12Ω,
R3与R4串联,R下=R3+R4=3.0+9.0=12Ω,
然后两部分并联后与R5串联,${R}_{并}=\frac{{R}_{上}{R}_{下}}{{R}_{上}+{R}_{下}}=\frac{12×12}{12+12}=6$Ω
${I}_{总}=\frac{E}{r+{R}_{并}+{R}_{5}}=\frac{12}{1+6+5}=1$A
由于两条支路的电阻值相等,所以电流也相等,${I}_{上}={I}_{下}=\frac{1}{2}{I}_{总}=0.5$A
R2两端的电压:U2=I上•R2=0.5×6.0=3V
R4两端的电压:U4=I下R4=0.5×9.0=4.5V
电容器的电压即为R2与R4的电压的差,则:UC=U4-U2=4.5-3=1.5V
电容器所带电荷量:${Q}_{1}=C{U}_{C}=4.0×1{0}^{2}×1{0}^{-6}×1.5=6×1{0}^{-4}$C
R的两端的电压大,可知电容器的下极板带正电.
(2)当电键S断开时,上边的支路被断开,没有电流,此时电容器两极板之间的电压等于R3两端的电压,其中上极板的电势高,所以上极板带正电.
此时的电流:$I′=\frac{E}{r+{R}_{3}+{R}_{4}+{R}_{5}}=\frac{12}{1+3+9+5}=\frac{2}{3}$A
R3两端的电压:${U}_{3}=I′•{R}_{3}=\frac{2}{3}×3=2$V
电容器的带电量:Q2=CUC′=CU3=4.0×102×10-6×2=8×10-4C
S断开后通过电阻R1的电荷量:$△Q={Q}_{1}+{Q}_{2}=6×1{0}^{-4}+8×1{0}^{-4}=1.4×1{0}^{-3}$C
答:(1)电容器所带电荷量是6×10-4C.
(2)将电键S断开,S断开后通过电阻R1的电荷量1.4×10-3C
点评 本题考查了含容电路问题,掌握含容电路的特点,分析找出电容器两端的电压再通过闭合电路欧姆定律进行求解是解答的关键.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | 0.5×10-2Wb | B. | 1.0×10-2Wb | C. | 0.5×10-1Wb | D. | 1.0 Wb |
 2010年10月1日,中国探月二期工程先导星“嫦娥二号”在西昌点火升空,准确入轨,赴月球拍摄月球表面影像、获取极区表面数据,如图所示,假设在地月转移轨道上运动时处于无动力状态,已知地球的质量为月球质量的81倍,当卫星进入地月转移轨道中速度最小时,它与月球中心和地球中心的距离之比为( )
2010年10月1日,中国探月二期工程先导星“嫦娥二号”在西昌点火升空,准确入轨,赴月球拍摄月球表面影像、获取极区表面数据,如图所示,假设在地月转移轨道上运动时处于无动力状态,已知地球的质量为月球质量的81倍,当卫星进入地月转移轨道中速度最小时,它与月球中心和地球中心的距离之比为( )| A. | 1:3 | B. | 1:9 | C. | 1:27 | D. | 9:1 |
| A. | 该质点总的运动是自由落体运动和圆周运动的叠加 | |
| B. | 该质点在磁场区域中所受的合力是一个恒力 | |
| C. | 该质点在磁场区域中所受的合力是一个大小不变,方向改变的力 | |
| D. | 该质点在磁场区域中所受的合力是重力和洛仑兹力的合力 |
 如图所示,竖直平面内有一电阻为R1、粗细均匀的光滑U形金属框BAHG,其中AH=l,AB=HG=$\frac{1}{2}$AH.在B、G处与宽度为l、电阻不计的平行光滑金属导轨BD、GE相接,DE之间接有电阻R2,已知R1=8R,R2=4R.在BG上方及CF下方有水平方向的匀强磁场,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从AH处由静止下落,在下落过程中导体棒始终保持水平,与金属框及轨道接触良好,设平行导轨足够长.已知导体棒下落$\frac{l}{4}$时的速度大小为v1,下落到BG处时的速度大小为v2.
如图所示,竖直平面内有一电阻为R1、粗细均匀的光滑U形金属框BAHG,其中AH=l,AB=HG=$\frac{1}{2}$AH.在B、G处与宽度为l、电阻不计的平行光滑金属导轨BD、GE相接,DE之间接有电阻R2,已知R1=8R,R2=4R.在BG上方及CF下方有水平方向的匀强磁场,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从AH处由静止下落,在下落过程中导体棒始终保持水平,与金属框及轨道接触良好,设平行导轨足够长.已知导体棒下落$\frac{l}{4}$时的速度大小为v1,下落到BG处时的速度大小为v2.