题目内容
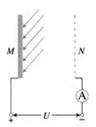
(8分)一长为L的细线,上端固定,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中。开始时,将细线与小球拉成水平,小球静止在A点,释放后小球由静止开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零。试求:
(1)A、B两点的电势差
(2)匀强电场的场强大小;
(3)小球到达B点时,细线对小球的拉力大小。
(1)  mgL/2q (2)
mgL/2q (2)  mg/q (3)
mg/q (3)  mg
mg
解析试题分析:(1)小球由A→B过程中,由动能定理:
mgLsin60°-qUAB=0
所以UAB= mgL/(2q)
mgL/(2q)
(2)E= =
= mg/q
mg/q
(3)小球在AB间摆动,由对称性知,B处细线拉力与A处细线拉力相等,而在A处,由水平方向平衡有
TA=Eq= mg
mg
所以TB=TA= mg
mg
或在B处,沿细线方向合力为零,有
TB=Eqcos60°+mgcos30°= mg。
mg。
考点:考查了动能定理,共点力平衡条件,电场力做功

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
探究能力是进行物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系,某同学采用了下述实验方法进行探索.如图所示,先让砂轮由动力带动匀速旋转,测得其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下,测出砂轮脱离动力到停止转动的圈数n,通过分析实验数据得出结论.另外已测试砂轮转轴的直径为2 cm,转轴间的摩擦力为10 N/π.经实验测得的几组ω和n如下表所示:
| ω/rad·s-1 | 0.5 | 1 | 2 | 3 | 4 |
| n | 5.0 | 20 | 80 | 180 | 320 |
| Ek | | | | | |
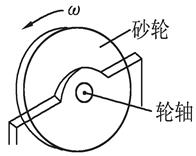
(1)计算出砂轮每次脱离动力的转动动能,并填入上表中.
(2)由上述数据推导出该砂轮的转动动能Ek与角速度ω的关系式为 .
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s,则它转过45圈时的角速度为 rad/s 。
 mg,将金属棒a从距水平面高度h处由静止释放。求:
mg,将金属棒a从距水平面高度h处由静止释放。求: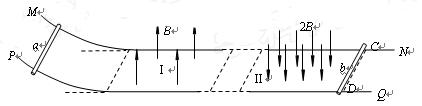
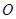 轴在竖直平面内无摩擦转动的细杆AB,两端分别固定质量1kg相等的两个球,已知OB=0.6m。现由水平位置自由释放,求:
轴在竖直平面内无摩擦转动的细杆AB,两端分别固定质量1kg相等的两个球,已知OB=0.6m。现由水平位置自由释放,求: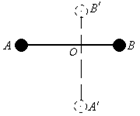
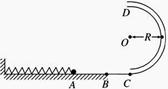

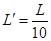 ,高度差为
,高度差为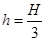 。若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为
。若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为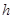 ,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变。
,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变。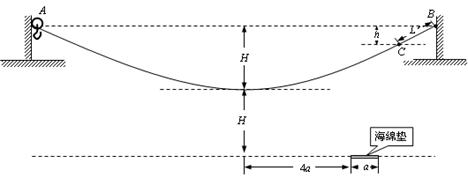
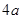 、宽度为
、宽度为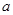 ,厚度不计的海绵垫子上。若参赛者由A点静止滑下,会落在海绵垫子左侧的水中。为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围?
,厚度不计的海绵垫子上。若参赛者由A点静止滑下,会落在海绵垫子左侧的水中。为了能落到海绵垫子上,参赛者在A点抓住挂钩时应具有初动能的范围?