题目内容
15.某人造卫星沿圆轨道运行,轨道半径是R,周期为T,(万有引力常量G为已知)估算地球质量为$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$.分析 人造地球卫星绕地球做匀速圆周运动,地球对卫星的万有引力提供卫星的向心力,根据牛顿第二定律计算地球的质量.
解答 解:设地球的质量为M,卫星的质量为m.根据牛顿第二定律得:
G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}R}{{T}^{2}}$
则有:$M=\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$
故答案为:$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$
点评 本题可总结为:知道环绕天体绕中心天体匀速圆周运动的轨道半径、周期,求出的不是环绕天体的质量,而是中心的质量.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.某一电场中的电场线和等势面分布如图所示,在电场中有A、B两点,下列说法中正确的是( )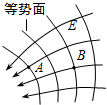

| A. | A点的电场强度比B点的电场强度小 | |
| B. | 负电荷在A点的电势能比在B点的电势能小 | |
| C. | A、B两点间的电势差UAB为正 | |
| D. | 负电荷由A向B移动,静电力做正功 |
1.下列关于合力和分力的说法,正确的是( )
| A. | 两个已知力的合力一定大于其中的任意一个力 | |
| B. | 两个已知力的合力可能比任意一个力都要小 | |
| C. | 一个已知力可以有多种分解方法,但各种情况的分力都是一样的 | |
| D. | 两个已知力的合力的结果有多种可能 |
 某实验小组应用如图1所示装置“探究加速度与物体受力的关系”,已知小车的质量为M,砝码及砝码盘的总质量为m,所使用的打点计时器所接的交流电的频率为50Hz.实验步骤如下:
某实验小组应用如图1所示装置“探究加速度与物体受力的关系”,已知小车的质量为M,砝码及砝码盘的总质量为m,所使用的打点计时器所接的交流电的频率为50Hz.实验步骤如下: