Question

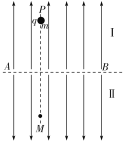
【题目】如图，空间有一竖直向下沿x轴方向的静电场，电场的场强大小按E＝kx分布(x是轴上某点到O点的距离)，k＝。x轴上，有一长为L的绝缘细线连接A、B两个小球，两球质量均为m，B球带负电，带电荷量为q，A球距O点的距离为L。两球现处于静止状态，不计两球之间的静电力作用。

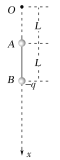
(1)求A球的带电荷量qA；

(2)剪断细线后，求B球的最大速度vm。

Answer 1

【答案】(1)－4q (2)

【解析】(1)A、B两球静止时，A球所处位置场强为

E1＝kL＝

B球所处的位置场强为E2＝k·2L＝

对A、B由整体法得：2mg＋qAE1－qE2＝0

解得：qA＝－4q

(2)当B球下落速度达到最大时，B球距O点距离为x0

mg＝qE＝qx0 解得：x0＝3L

运动过程中，电场力大小线性变化，所以由动能定理得：

mgL－qL＝－0

q＝＝mg

解得：vm＝