Question

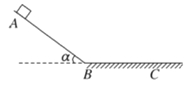
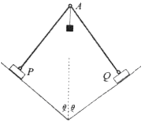
【题目】如图所示，对称、粗糙斜面与竖直方向夹角θ=53°，硬质轻杆通过铰链与两个相同且质量为m1=1.0kg的物块P、Q相连，对称放在斜面上，一质量m2=1.6kg的物体悬挂在铰链A上，对称调节P、Q的位置，使杆与斜面垂直，整个装置处于平衡状态，设最大静止摩擦力等于滑动摩擦力，g=10m/s2，sin53°=0.8，cos53°=0.6，求：

(1)杆对物块P的作用力；

(2)物块与斜面间动摩擦因数的最小值；

(3)若斜面光滑，对称调节P、Q的位置，使整个装置仍处于平衡状态，求此时杆与水平方向夹角的正切值．

Answer 1

【答案】(1)10N(2) (3)

【解析】

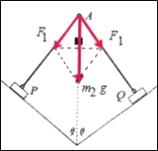
(1)A点受到的绳子的拉力等于质量为物体的重力，其沿杆的方向的分量等于杆对P的作用力，如图，则：

所以杆对P的作用力等于

(2)对P进行受力分析，如图

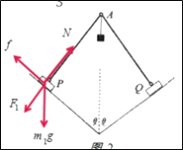
当静摩擦力恰好为最大值时，对应动摩擦因数最小值，设为

沿杆的方向上有：

沿斜面方向有：

并且有：

联立解得

(3)斜面光滑，对称调节P、Q的位置，使整个装置平衡，如图．

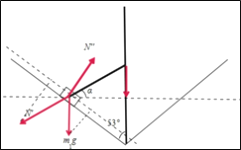
设杆与水平方向夹角为，

在沿斜面方向上有：

杆的压力等于质量为的物体的重力沿杆的方向上的分量，有：

联立解得：