题目内容
19.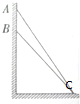 如图所示,位于竖直平面内的一长木板斜靠在竖直墙上的A点,其与水平面的夹角为53°,另一同样材料的长木板斜靠在竖直墙上的B点,其与水平面的夹角为45°,两长木板底端都在C点处.若将一小球从A点由静止释放,小球运动到C点历时为t,将同-小球从B点由静止释放,小球运动到C点历时也为t,则小球与长木板间的动摩擦因数为(sin53°=0.8,cos53°=0.6)( )
如图所示,位于竖直平面内的一长木板斜靠在竖直墙上的A点,其与水平面的夹角为53°,另一同样材料的长木板斜靠在竖直墙上的B点,其与水平面的夹角为45°,两长木板底端都在C点处.若将一小球从A点由静止释放,小球运动到C点历时为t,将同-小球从B点由静止释放,小球运动到C点历时也为t,则小球与长木板间的动摩擦因数为(sin53°=0.8,cos53°=0.6)( )| A. | $\frac{1}{7}$ | B. | $\frac{3}{14}$ | C. | $\frac{3\sqrt{2}}{8}$ | D. | $\frac{5\sqrt{2}}{8}$ |
分析 分别对两种情况进行分析,根据牛顿第二定律及运动学公式列式,联立即可求得动摩擦因数.
解答 解:设木板与水平面的夹角为θ,则由牛顿第二定律可知:
mgsinθ-μmgcosθ=ma;
解得:a=gsinθ-μgcosθ
设C距墙的距离为d,则下落的距离为$\frac{d}{cosθ}$;
由位移公式可得:
$\frac{d}{cosθ}$=$\frac{1}{2}$at2;
即t=$\sqrt{\frac{2d}{cosθ(gsinθ-μgcosθ)}}$
因θ为45°时和53°时时间相等,则有:
cos45°(gsin45°-μgcos45°)=cos53°(gsin53°-μgcos53°)
解得:
μ=$\frac{1}{7}$
故选:A.
点评 本题考查牛顿第二定律的应用,要注意明确几何关系的确定,注意设定的中间量为两种情况下的相同量d.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.电视机的玻璃荧光屏表面经常有许多灰尘,这主要是因为( )


| A. | 灰尘的自然堆积 | |
| B. | 电视机工作时,屏表面有静电而吸咐灰尘 | |
| C. | 电视机工作时,屏表面温度较高而吸附灰尘 | |
| D. | 玻璃有较强的吸附灰尘的能力 |
15. 如图所示,倾角为30°的斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{g}{2}$(g为重力加速度)向上加速运动距离x的过程中,下列说法正确的( )
如图所示,倾角为30°的斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{g}{2}$(g为重力加速度)向上加速运动距离x的过程中,下列说法正确的( )
 如图所示,倾角为30°的斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{g}{2}$(g为重力加速度)向上加速运动距离x的过程中,下列说法正确的( )
如图所示,倾角为30°的斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{g}{2}$(g为重力加速度)向上加速运动距离x的过程中,下列说法正确的( )| A. | 重力势能增加mgs | B. | 动能增加$\frac{1}{4}$mgs | C. | 机械能增加mgs | D. | 拉力做功为$\frac{1}{2}$mgs |
 如图所示,公路AB与BC相互垂直,且已知AB=100m,甲车从A点以8m/s的速度沿AB行驶,乙车同时从B点以6m/s的速度沿BC行驶,问两车相距的最近距离是多少?
如图所示,公路AB与BC相互垂直,且已知AB=100m,甲车从A点以8m/s的速度沿AB行驶,乙车同时从B点以6m/s的速度沿BC行驶,问两车相距的最近距离是多少?