题目内容
【题目】光滑水平平台AB上有一根轻弹簧,一端固定于A,自然状态下另一端恰好在B。平台B端连接两个内壁光滑、半径均为R=0.2m的1/4细圆管轨道BC和CD。D端与水平光滑地面DE相接。E端通过光滑小圆弧与一粗糙斜面EF相接,斜面与水平面的倾角θ可在0°≤θ≤75°范围内变化(调节好后即保持不变)。一质量为m=0.1kg的小物块(略小于细圆管道内径)将弹簧压缩后由静止开始释放,被弹开后以v0=2m/s进入管道。小物块与斜面的滑动摩擦系数为![]() ,取g=10m/s2,不计空气阻力;
,取g=10m/s2,不计空气阻力;
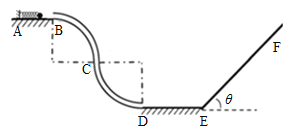
(1)求物块过B点时对细管道的压力大小和方向;
(2)当θ取何值时,小物块在EF上向上运动的时间最短?求出最短时间。
(3)求θ取不同值时,在小物块运动的全过程中产生的摩擦热量Q与tanθ的关系式。
【答案】(1)1N,方向竖直向上(2)0.3s(3)![]()
【解析】(1)设轨道对物块的压力竖直向下,由牛顿第二定律得: ![]()
解得:F=1N
由牛顿第三定律,物块对轨道的压力大小为![]() ,方向竖直向上
,方向竖直向上
(2)物块到达DE时的速度为v,根据动能定理得: ![]()
解得: ![]()
沿斜面上滑,根据牛顿第二定律得: ![]()
上滑时间为: ![]()
联立可得: 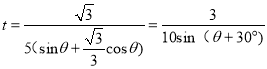
由数学知识可得,当![]() 时,有
时,有![]()
(3)物块恰好能在斜面上保持静止,根据平衡条件有: ![]() ,
, ![]() ,则当
,则当![]() ,滑块在EF上停下后即保持静止
,滑块在EF上停下后即保持静止
在EF上滑行的距离为: ![]() ,产生的摩擦热量为:
,产生的摩擦热量为: ![]()
化简得: 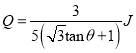
当![]() ,滑块在EF上停下后返回,经多次往复运动后,最终静止于E点
,滑块在EF上停下后返回,经多次往复运动后,最终静止于E点
产生的摩擦热量为: ![]()

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目