��Ŀ����
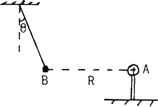
����Ŀ����ͼ��ʾ��MN��һ������ֱƽ���ڰ뾶Ϊ1 m�Ĺ⻬��1/4Բ�����������ϴ���ˮƽ���ҵ���ǿ�糡��������Ҳ���һ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��Ϊ![]() ��0.1 T������һ�������Ϊ0.1 C������Ϊ10 g�Ĵ�����С���M���ɾ�ֹ��ʼ�����»���ǡ����NP������ֱ���˶�����֪EF���ĵ�ѹΪ
��0.1 T������һ�������Ϊ0.1 C������Ϊ10 g�Ĵ�����С���M���ɾ�ֹ��ʼ�����»���ǡ����NP������ֱ���˶�����֪EF���ĵ�ѹΪ![]() ��2 V��������d��2 m��EF�������з���ֱֽ�������Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪ
��2 V��������d��2 m��EF�������з���ֱֽ�������Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪ![]() ��ABCD��һ�߳�ΪL��1m�������κУ����߾�Ϊ�⻬��Ե�壬�е�AB��ǡ����ų�����߽��غϡ���AB�ߵ��е���һС��Q��С��Q��N��P��ͬһ��ˮƽֱ���ϣ�����С��ǡ�ܴ�С��Q���������κ��ڣ�����С�����Ե����ײʱ����ʧ���ܣ����ٶȷ���gȡ10 m/s2������
��ABCD��һ�߳�ΪL��1m�������κУ����߾�Ϊ�⻬��Ե�壬�е�AB��ǡ����ų�����߽��غϡ���AB�ߵ��е���һС��Q��С��Q��N��P��ͬһ��ˮƽֱ���ϣ�����С��ǡ�ܴ�С��Q���������κ��ڣ�����С�����Ե����ײʱ����ʧ���ܣ����ٶȷ���gȡ10 m/s2������
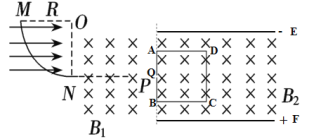
��1��С���˶���N��ʱ���ٶ�v.
��2��С���˶���N��ʱ�������͵糡���Ĺ��ʷֱ�Ϊ���٣�
��3��Ϊ��֤����С���������κеıڷ��������ײ�����ܴ�С��Q�뿪�����Ҳ���ǿ�ų��ĴŸ�Ӧǿ��![]() �Ĵ�СΪ���٣�
�Ĵ�СΪ���٣�
���𰸡���1��10m/s����2��0��4W����3��4n+2��T������n=0��1��2����������4k��T������k=1��2������
��������
��1��С����NP��ֱ���˶�����ƽ�������ɵã�mg=qvB1
�������ݽ�ã�v=10m/s��
��2��С���M�㵽N��Ĺ����У��ɶ��ܶ����ã�mgR+qER=![]() mv2��
mv2��
�������ݽ�ã�E=4N/C��F��=0.4N��
�������ٶȴ�ֱ���������Ĺ���Ϊ��PG=0
�糡���ķ������ٶ�ͬ����糡���Ĺ���Ϊ��PE=Eqv=4��0.1��10W=4W��
��3���ڰ�临�ϳ���С���ܵ糡��Ϊ��![]() ��0.1N��mg��������ƽ�⣮
��0.1N��mg��������ƽ�⣮
��С��������Բ���˶������˶��뾶ΪR������qvB2��m![]() �ã�R�䣽
�ã�R�䣽![]() ��
��
��ʹ�������ܴ�Q�״���������ӵ��˶��켣�����������������
���ݼ��ι�ϵ֪��![]() ����n=0��1��2������
����n=0��1��2������
��ã�![]() ����n=0��1��2������
����n=0��1��2������
���ݼ��ι�ϵ֪��![]() ����k=1��2������
����k=1��2������
��ã�![]() ����k=1��2������
����k=1��2������

 ���ݼ���ϵ�д�
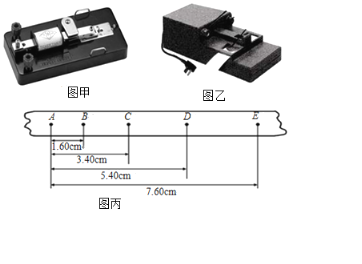
���ݼ���ϵ�д�����Ŀ��������̽�����ٶ������������Ĺ�ϵ����ʵ��ʱ���������ֽ���ļ��ٶȺ���õķ�ӳ���ٶ�a����F�Ĺ�ϵ���й����ϼ�¼�ڱ�1�У�����õķ�ӳ���ٶ�a������M�Ĺ�ϵ���������ڱ�2��
��1
a/��ms��2�� | 1.98 | 4.06 | 5.95 | 8.12 |
F/N | 1.00 | 2.00 | 3.00 | 4.00 |
��2
a/��ms��2�� | 2.04 | 2.66 | 3.23 | 3.98 |
| 0.50 | 0.67 | 0.80 | 1.00 |
����ͼ���������ݣ��ֱ���a��F��a��![]() ͼ��
ͼ��

��1����ͼ������ж�����Mһ��ʱ��a��F�Ĺ�ϵΪ_____����Fһ��ʱ��a��M�Ĺ�ϵΪ_____����������������
��2����a��Fͼ���֪M��_____kg��
��3����![]() ͼ���֪F��_____N��
ͼ���֪F��_____N��